ว่าด้วยเรื่องสถิติ 6 : ไคว์สแคว์ ภาคสมบูรณ์
ผมสรุปวิธีใช้ ไคว์สแคว์อีกครั้งนะครับ
- ใช้กับข้อมูลที่เก็บเป็นนามบัญญัติ ก็คือเก็บเป็นตัวอักษร
- ตัวแปรเป็นอิสระไม่ขึ้นต่อกัน
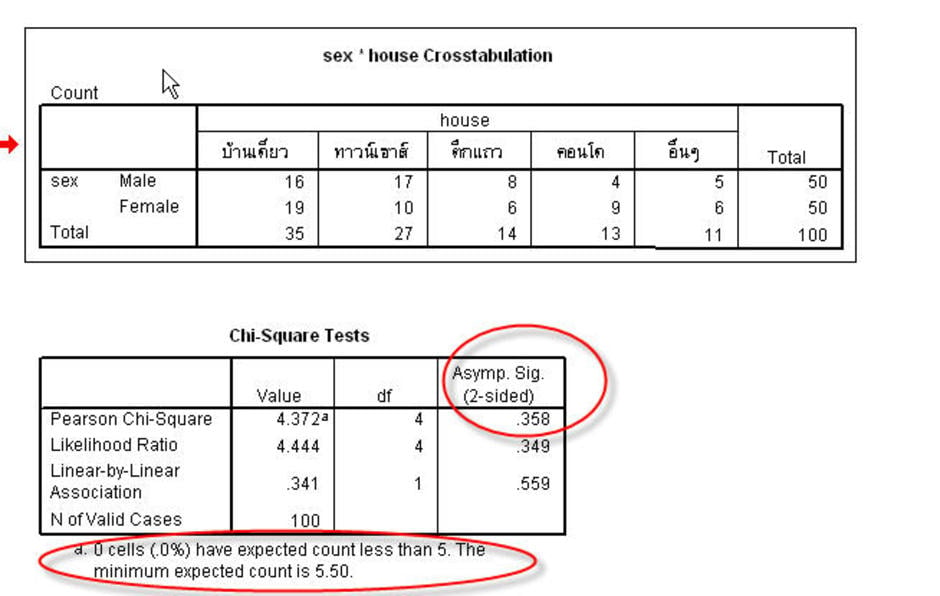
- เวลาใช้ก็ให้ดูว่ามีอยู่กี่ช่องที่มีค่าคาดหวังน้อยกว่า 5 ถ้ามีน้อยกว่าร้อยละ 20 ของจำนวนช่องทั้งหมด ก็ถือว่าผ่านครับไปข้อต่อไป
- ดูค่า p value เทียบกับ 0.05 ถ้ามากกว่า 0.05 แสดงว่าตัวแปรที่ 1 กับตัวแปรที่ 2 ไม่มีความแตกต่างอย่างมีนัยสำคัญครับ แต่ถ้าหากได้ค่าน้อยกว่า 0.05 แสดงว่าตัวแปรที่ 1 กับตัวแปรที่ 2 มีความแตกต่างอย่างมีนัยสำคัญครับ
นั่นเป็นขั้นตอนการวิเคราะห์ค่าไคว์สแคว์ แล้วมีคำถามตามมาตอนนี้คือ
- แล้วถ้าเวลาเราเหลือบไปดูค่าคาดหวังแล้วพบว่ามันมีค่าน้อยกว่า 5 อยู่มากกว่าร้อยละ 20 ของจำนวนช่องทั้งหมดล่ะต้องทำอย่างไร
- แล้วถ้ายุบตารางลงไปต่ำสุดแล้วเหลืออยู่ 2 x 2 แล้วยังมีช่องที่มีค่าคาดหวังน้อยกว่า 5 อยู่อีกละครับต้องทำอย่างไร
แต่ถ้าตัวอย่างเราไม่มากนักคือ ไม่มากขนาดไหนไม่มีใครเขาระบุไว้ชัดเจน แต่เท่าที่ผมค้นดูตัวอย่างจากหลายๆที่ ก็เอาเป็นว่า น้อยกว่า 30 ลงมาก็แล้วกัน ก็ให้คำนวนด้วยค่า Fisher’s Exact Test ซึ่งก็จะใช้กับเฉพาะตาราง 2x2 เท่านั้นเหมือนกัน อย่างในรูปข้างบนเป็นการคำนวณจากตาราง 5x2 ค่าตัวนี้ก็เลยไม่ขึ้นมาครับ ค่า Fisher's Exact Test นี้ จริงๆ แล้วมันก็ใช้ได้เหมือนไคว์สแคว์แหละครับ แต่สูตรการคำนวณนี้สุดแสนจะเจ็บปวดครับ มันต้องทำ factorial ซะปวดหัวเลย ก็เลยไม่มีใครอยากใช้เวลาตัวอย่างมากๆ หนีไปใช้ค่า chi square ง่ายกว่าเยอะ แต่พอในรายที่ไม่ผ่านข้อกำหนดของไคว์สแคว์ ก็แล้วตัวอย่างไม่มากนัก ก็เลยถูกบังคับให้ใช้ค่า Fisher's Exact Test นี้ สนใจอ่านเพิ่มเติมค่า Fisher’s Exact Test ได้ที่นี่ครับ
[หมายเหตุ ค่าตัวเลข 30 เป็นค่าประมาณจากประสบการณ์ส่วนตัวครับ เพราะตัวเลขยิ่งเยอะยิ่งคำนวณยากครับ]
- แล้วถ้าเป็นตัวแปรแบบตัวอย่างข้างบน คือดูแล้วมันยุบช่องไม่ได้ล่ะ ต้องทำอย่างไร
- คำถามสุดท้าย ไม่ว่าจะคำนวณค่า ไคว์สแคว์ , Yates’ chi square หรือว่า Fisher’s Exact test ไม่เห็นมันจะมีค่าเท่ากันเลยสักอัน อย่าว่าแต่ค่าเท่ากันเลยนะครับ แม้แต่ค่า p value ของแต่ละตัวยังไม่เห็นจะเท่ากันเลย
ผมคิดว่าเรื่องไคว์สแคว์นี้ ผมคงเขียนจบแล้วโดยสมบูรณ์ หรือท่านคิดว่าอย่างไรครับ กลับไปนั่งอ่านดูอีกรอบ เอ! ทำไมเรายิ่งเขียนยิ่งหนักขึ้นหนอ เฮ้อ! ก็อย่างนี้แหละครับ สถิติ มีหนักมีเบา เป็นธรรมดาของโลก
ความเห็น (11)
![]() อรุณสวัสดิ์ค่ะคุณไมโต
อรุณสวัสดิ์ค่ะคุณไมโต
- เช้าวันนี้หัวหนักจังเลย ยังไม่ค่อยรู้เรื่องครูไมโตสอนเลยค่ะ
- ตอนแรกเข้าใจ พอถึงบ้านในฝันตรงนั้นยังเข้าใจอยู่พอมาถึงใต้ตารางการยอมรับเริ่มเขวแล้ว
- ค่ะครูไมโตสอนดีมากแต่นักเรียนปึกเองค่ะ
- ปัวซองสแคว์ คล้ายๆกับครัวซองสแคว์ที่คาร์ฟูหรือเปล่าคะ อิอิ ยิ้มยิ้ม พูดเล่น
- อย่างไรก็ตามนักเรียนคนนี้จะเข้ามาอ่านให้เข้าใจจนได้ค่ะ ครูไมโต ขอบคุณมากค่ะ
- นั่นสิครับครูอ้อย ยิ่งเขียนผมก็รู้สึกว่ายิ่งหนักเหมือนกัน
- ถ้าจะเอาเป็นแบบพูดให้รู้จัก ก็จะเป็นว่า ถึงเวลาจริงเอาไปใช้ไม่ได้
- แต่ถ้าจะอธิบายให้เห็นจริง มันมีขั้นตอนเยอะ อย่างเรื่องไคว์สแคว์นี้เป็นเพียงตัวอย่างแรก มันมีรายละเอียดปลีกย่อยเยอะ
- อะไรที่มันย่อยไปมากๆ ผมก็ตัดทิ้งครับ
- เวลาครูอ้อยอ่านสถิติครับ ให้เสียเวลาทำความเข้าใจกับตัวอย่างให้มาก พอเข้าใจเสร็จปุ๊บ ก็ลืมมันซะให้หมด แล้วมาจำเพียงแค่ว่า มันคืออะไร ใช้เมื่อไหร่ มีข้อจำกัดในการใช้อย่างไร ถ้าไม่ได้ตามข้อจำกัดแล้วจะแก้ไขอย่างไร เท่านั้นก็พอครับ อย่างตัวอย่างข้างบนนั้นถ้าจำแค่นี้ก็ไม่เยอะ นะครับ เพียงเวลาเขียนต้องอธิบายเยอะหน่อยเท่านั้นครับ เพื่อให้เข้าใจกระจ่างขึ้น
- ครูอ้อยมีวิธีการจำคล้ายๆผมเลยครับ ผมก็จะเลือกแปลงให้มันคล้ายๆ กับของที่เคยรู้จัก เราก็จะจำมันได้ เหมือนเอาเส้นเชือกผูกไว้ไปไหนก็ไปด้วยกัน อย่างปัวซองกับคัวซองที่คาร์ฟู ของครูอ้อยนี่แหละครับ
- เอาไว้ครูอ้อยเริ่มเรียนวิชานี้เมื่อไหร่ก็จะเข้าใจเองครับ (ไปเข้าใจตอนก่อนสอบเหมือนผมเลย)
- ผมคงเป็นครูที่ไม่ค่อยจะดีเท่าไหร่ เพราะเวลาพูดจะมีแต่น้ำซะมากกว่า นักเรียนต้องหาแห หา สวิงกันมาเองนะครับ
- เช้านี้ อากาศสดใสครับ แสงแดดจัดกำลังดี ท้องฟ้าแจ่มใส เดี๋ยวต้องไปทำงานครับ แล้วตอนบ่ายค่อยแว๊บไปเดินเล่น
- Bright lily ไม่รู้เรื่องหรอกค่ะ รู้อย่างเดียวขายบ้าน กับสระว่ายน้ำ
- ทำ excel เป็นแค่บวก ลบ คูณ หาร หรือ forecast เป้าหมายเป็นแค่นั่นล่ะค่ะ
- แต่เป็นองค์ความรู้ที่ดีมากนะคะ
สวัสดีตอนบ่ายครับ คุณ Bright lily
- ทำอย่างที่คุณ Bright lily ทำเป็นอย่างนั้นดีแล้วครับ ได้ตังเยอะดี ทำอย่างที่ผมทำอยุ่ไม่ค่อยจะได้ตังหรอกครับ แต่ได้ความสนุก ได้ทำในสิ่งที่อยากทำ
- สิ่งพวกนี้เป็นพื้นฐานของการวิเคราะห์ทางสถิติ ที่ช่วยแยกของออกจากกันอย่างชัดเจน เวลาดุด้วยตาเปล่าแล้วตัวเลขมันจะหลอกตาครับ ก็ต้องใช้เรื่องการวิเคราะห์พวกนี้เข้ามาช่วย ทำให้มั่นใจได้มากขึ้น
ป้ามหาภัย นักเรียนPh.D.ด้วยคน
ขอบคุณสำหรับข้อความดีๆเข้าใจง่าย
กำลังอยู่ในช่วงศึกษา ไคว์สแควร์และคอสแทบคะ
จะขอมาเป็นลูกศิษย์อีกคน
อยากให้อธิบายจุดนี้เพิ่มเติมคะ
ค่าคาดหวังในที่นี้เป็นค่าที่เครื่องคำนวนให้ ไม่ใช่ค่าข้อมูลดิบที่เราเห็นในตาราง
แล้วไอ้ตัวเลขที่กรอกในตาราง5*2 นั้นได้มาจากร้อยละหรือคะ
สวัสดีค่ะคุณไมโต
- ครูอ้อยเรียนแล้วค่ะ..กลับมาอ่านอีกจึงเข้าใจ..หากกลับไปอ่านอีก ก็จะเข้าใจยิ่งขึ้นค่ะ
- เมื่อไหร่จะเขียนอีกล่ะคะ
ขอบคุณค่ะ
ผู้ความรู้น้อย
สวัสดีค่ะ ขอถามเพิ่มเติมนะคะ
ถ้าเรามีแบบสอบถามที่ถามถึงความคิดเห็นของการปฏิบัติที่ไม่เหมาะสม 2 ด้าน คือด้านร่างกาย กับด้านจิตใจ โดยแต่ละด้านมีคำถามย่อย ๆ ประมาณ 5 ข้อ การวัด มี 3 ระดับ คือ ไม่เคย บางครั้ง บ่อย
ตัวอย่างเช่น
การปฏิบัติด้านร่างกาย |
ความคิดเห็น | ||
| ไม่เคย | บางครั้ง | บ่อย | |
| ตี | X | ||
|
|
||||||||
แปลความหมายได้ว่า ไม่เคยคิดว่าจะถูกตีมาก่อน
แล้วหากจะหาความสัมพันธ์ระหว่างความคิดของการได้รับการปฏิบัติที่ไม่เหมาะสมของด้านร่างกายกับด้านจิดใจ ที่คิดไว้ว่าน่าจะต้องใช้ ไคฯ เพราะข้อมูลถูกวัดมาในระดับนี้ จะทำอย่างไร จับคู่เป็นข้อย่อยไปทุกคู่ หรือต้องปรับ data ใหม่ให้ข้อย่อยเหล่านั้น ทำใหม่ให้เป็น 1 เดียว
หรือแนวคิดผิดมาตั้งแต่ต้นแล้ว ควรใช้สถิติตัวอื่น
ช่วยหน่อยเถอะค่ะ งง...แล้ว
ถ้าเป็นตารางมากกว่า 2x2 ไม่ผ่านข้อตกลงเบื้องต้นกรณีมีค่าน้อยกว่า 5 มากกว่าร้อยละ 20 และไม่สามารถยุบเซลได้ต้องใช้ค่าใดแทนไคสแควร์
เนื้อหาอ่านแล้วสนุกมาเลยครับ คอยติดจามมาเรื่อยๆเลย แต่รูปภาพบางรูปนั้นไม่ขึ้นแล้ว อาจจะเนื่องจากลิ๊งนั้นนานมากแล้ว ยังไงช่วยรบกวนแก้ไขหน่อยจะดีมากเลยครับ
ผมแก้ไข link ที่เกี่ยวข้องให้แล้วครับ ขอบคุณมากครับ