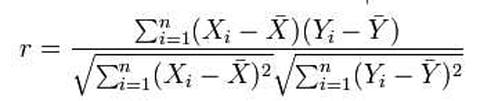เรียนสถิติด้วยภาพ ตอนที่ 16 สัมประสิทธิ์สหสัมพันธ์ (1)
สัมประสิทธิ์สหสัมพันธ์ หรือ Pearson's correlation coefficient (ย่อ r) มีคนอธิบายโดยใช้แนวคิดที่หลากหลายมาก
โดยส่วนตัวผมเอง จะชอบแนวคิดเรื่องการอธิบายโดยเวกเตอร์ทางฟิสิกส์
แนวคิดเวกเตอร์คือ ถ้าเรามีลูกศร X ชี้ไปทางหนึ่ง และ Y ชี้ไปอีกทางหนึ่ง จะมีการนิยามว่า r คือค่า cosine ของมุมระหว่างสองเวกเตอร์นี้ ซึ่งค่า cosine ดังกล่าว เป็นตัวชี้วัด การชี้ไปทิศทางเดียวกันของสองเวกเตอร์
สองเวกเตอร์ชี้ไปทางเดียวกันแค่ไหน ก็แค่ลอง
คูณเวกเตอร์แบบ dot product เทียบกับกรณีที่ให้สองเวคเตอร์นั้นชี้ไปทางเดียวกันอย่างสมบูรณ์ อัตราส่วนนี้จะบอกถึงมุมระหว่างกัน คือถ้าชี้ไปทางเดียวกันจะมีค่าเป็น 1 หรือสวนกัน มีค่าเป็น -1 หรือถ้าตั้งฉากกัน จะมีค่าเป็นศูนย์
หรือนั่นคือ ถ้าข้อมูลเช่น เหตุ (X) และ ผล (Y) มาพล็อตกัน แล้วเกิดการดึงรั้งกันไปทางเดียวกัน แสดงว่า เกิดการชี้ไปทิศทางเดียวกันของสองเวกเตอร์ แต่จะชี้ไปทางเดียวกันรุนแรงแค่ไหน ก็ขึ้นกับข้อมูลดิบ
สมมติแกนนอนคือ เหตุ (X) และแกนยืนคือ ผล (Y) เราพล็อตกราฟลงจุด จะเห็นทำนองนี้
ถ้าตัวแปรเหตุ กับ ตัวแปรผล ไปกันคนละทิศละทาง อาจกล่าวได้ว่า ต่างคนต่างไป เป็นเอกเทศต่อกัน ภาษาเวกเตอร์จะบอกว่า เวกเตอร์ตั้งฉากกัน (orthogonal) คือไม่ยอมไปร่วมกันในทางเดียวกันแม้แต่น้อย ซึ่งมุม 90 องศามีค่า cosine เป็นศูนย์ หรือนั่นคือ กรณีนี้ ค่า r = 0
ลองดูอีกกรณีหนึ่ง เมื่อ r มีค่าเป็นบวก (มากกว่าศูนย์) ซึ่ง cosine ที่มีค่ามากกว่าศูนย์คือ กรณีที่เวกเตอร์ทั้งสอง เริ่มชี้ไปทิศเดียวกัน ซึ่งมุมที่สองเวกเตอร์กระทำต่อกัน จะต้องอยู่ระหว่าง 0 ถึง 90 องศา
ระวัง ! คำว่า เวกเตอร์ทำมุมต่อกัน ไม่ใช่มุมเอียงของรูป เรามองไม่เห็นการทำมุมต่อกันด้วยตาตรงนี้ แต่ได้จากการคำนวณเท่านั้น มันเป็นความสัมพันธ์แบบซ่อนเร้น ส่วนมุมที่ดูในรูปนี้ ไม่ได้บอกอะไร เพราะขึ้นกับผมใช้สเกลแกนยืนกับแกนนอนเป็นอย่างไรด้วย เช่น หากยืดแกนนอนให้ยาวมาก ก็เห็นมุมเอียงลาดเกือบนอน หรือหากยืดแกนยืนให้ยาว เราจะเห็นกราฟชี้เกือบชัน จึงขอให้ตระหนักว่า "เวกเตอร์ทำมุมต่อกัน ไม่ใช่มุมเอียงของรูป"
คำว่า เวกเตอร์ทำมุมต่อกันในที่นี้ จึงบอกว่า ข้อมูลทั้งหมด ถูกร้อยเป็นเส้นร่วมเรียงกันได้ดีแค่ไหน (collinearity)
 สองเวกเตอร์ทำมุม 60 องศาต่อกัน มีค่า r 0.5
สองเวกเตอร์ทำมุม 60 องศาต่อกัน มีค่า r 0.5
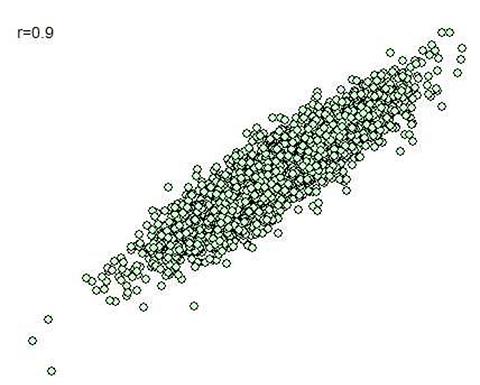 สองเวกเตอร์ทำมุม 25.8 องศาต่อกัน มีค่า r 0.9
สองเวกเตอร์ทำมุม 25.8 องศาต่อกัน มีค่า r 0.9
 สองเวกเตอร์ทำมุม 8.1 องศาต่อกัน มีค่า r 0.99
สองเวกเตอร์ทำมุม 8.1 องศาต่อกัน มีค่า r 0.99
สองเวกเตอร์ไม่จำเป็นต้องไปทางเดียวกันก็ได้ อาจไปแบบสวนทางกันก็ได้ ดังนี้
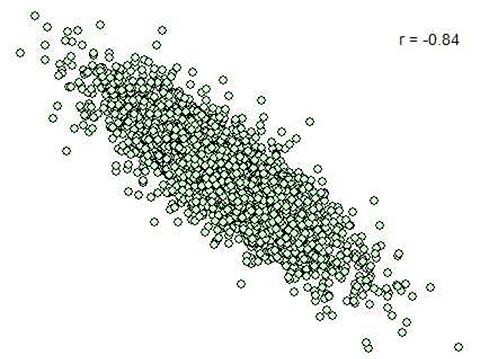 สองเวกเตอร์ทำมุม -32.9 องศาต่อกัน มีค่า r -0.84
สองเวกเตอร์ทำมุม -32.9 องศาต่อกัน มีค่า r -0.84
บางคนอาจใช้ค่า r ยกกำลังสอง เรียก R-square ก็จะได้ค่าที่เป็นบวกเสมอ ระหว่างศูนย์กับหนึ่ง โดยตีความว่า R-square สูง ๆ แสดงว่าข้อมูลสามารถร้อยเป็นเส้นเดียวกันได้สวยงาม ถ้าค่าต่ำ คือกระเจิง
สนใจอ่าน เรียนสถิติด้วยภาพ แบบครบทุกตอน เข้าไปที่
ความเห็น (4)
ก่อนอื่นขอขอบคุณสำหรับบทความดีๆ ที่อ่านเข้าใจง่าย
อยากรบกวนสอบถามเพิ่มเติมค่ะ เรื่อง
ความแตกต่างของ absolute precision กับ relative precision
แล้วทั้ง 2 ค่านี้ สามารถนำมาใช้คำนวณขนาดตัวอย่างได้อย่างไรค่ะ
ขอบคุณค่ะ
ขอบคุณอาจารย์มากมากค่ะ
ดีใจที่ผ่านมาๆด้อ่านค่ะ
ขอบพระคุณอาจารย์อย่างสูงค่ะ ชอบทุกบทความเลย