Odds Ratio เปลี่ยนจาก 1.88 เป็น 1 เมือวิเคราะห์แยก (Stratified) ด้วยกลุ่มอายุ, กลุ่มอายุเป็น Confounder

การอ้วนไม่ได้ทำให้การป่วยมากขึ้น Odds Ratio เปลี่ยนจาก 1.88 เป็น 1 ถ้า Stratified ด้วยกลุ่มอายุ กลุ่มอายุน้อยป่วยเป็น 3 เท่าของกลุ่มอายุมาก

Observational study มีตัวแปรคือ โรค, การอ้วนและกลุ่มอายุ
โรค "y" เป็นตัวแปรตาม 
ป่วย y=0
ไม่ป่วย y=1
การอ้วน "x" เป็นตัวแปรต้น  
อ้วน x=0  
ไม่อ้วน x=1
ตัวเลขจำนวนนับที่จะนำมาถ่วงน้ำหนักแต่ละกลุ่มคือ pop
อายุน้อย =<  45 ปี gr=0
อายุมาก > 45 ปี gr=1

STATA จะเรียงค่าตัวแปรจากน้อยไปมาก

	x=0	x=1
y=0	0, 0	0, 1
y=1	1, 0	1, 1

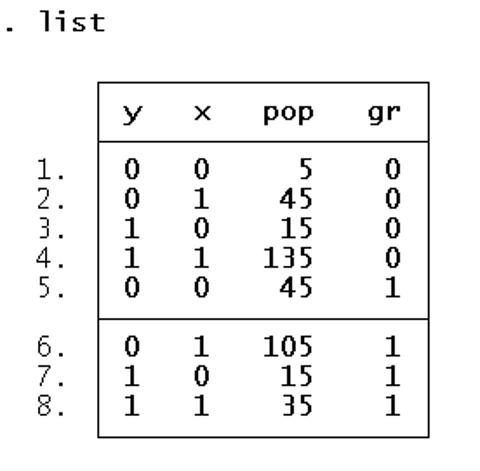
ถ้ายังไม่แยกกลุ่มอายุ (เทียบได้กับการรวมกัน แบบ Crude)
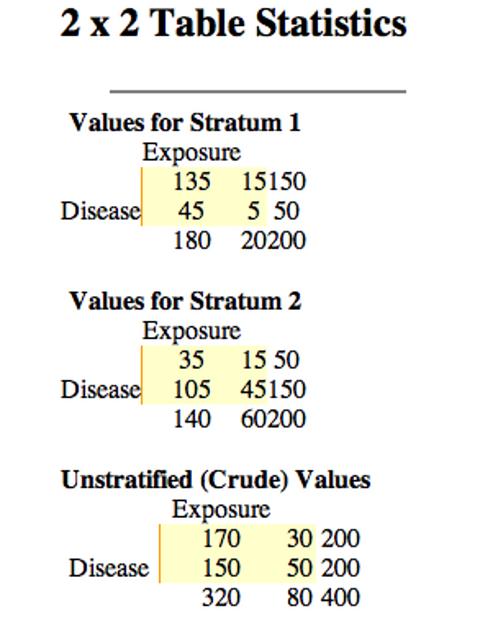
Case 200 คนคือกลุ่มป่วย ก่อนป่วยอ้วน 170 คน ก่อนป่วยไม่อ้วน 30 คน
Control 200 คนคือกลุ่มไม่ป่วย ก่อนป่วยอ้วน 150 คน ก่อนป่วยไม่อ้วน 50 คน

	อ้วน Exposed	ไม่อ้วน Unexposed
ป่วย Cases	170	30
ไม่ป่วย Controls	150	50

Odds_1 = 170 / 30
Odds_2 = 150 / 50
Odds Ratio = Odds_1 / Odds_2 = (170 / 30) / (150 / 50)
Odds Ratio = (170 x 50) / (150 x 30)  = 1.88

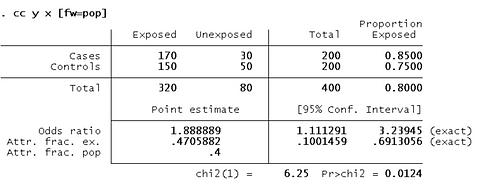
คำสั่งใน STATA คือ cc y x [fw=pop]
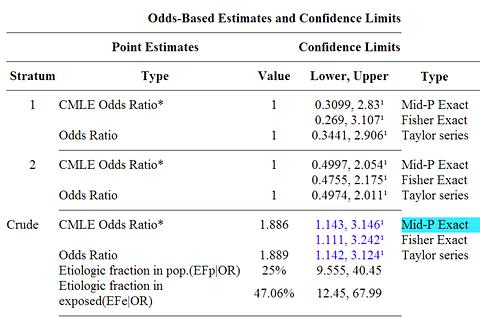
ซึ่งได้ค่า Odds Ratio =1.88  และ 95% Conf. Interval 1.11 to 3.23
คนอ้วนป่วยมากกว่าคนไม่อ้วน 1.88 เท่า

กลุ่มอายุ gr= 0 และ gr=1
แยกวิเคราะห์โดยใช้ตัวแปรกลุ่มอายุ Stratified analysis โดยตัวแปร "gr"

gr_0	อ้วน	ไม่อ้วน
ป่วย	135	15
ไม่ป่วย	45	5

Odds Ratio = (135 x 5) / (45 x 15) = 1

gr_1	อ้วน	ไม่อ้วน
ป่วย	35	15
ไม่ป่วย	105	45

Odds ratio = (35 x 45) / (105 x 15) = 1

คำสั่งใน STATA คือ
cc y x [fw=pop] if gr==0
cc y x [fw=pop] if gr==1

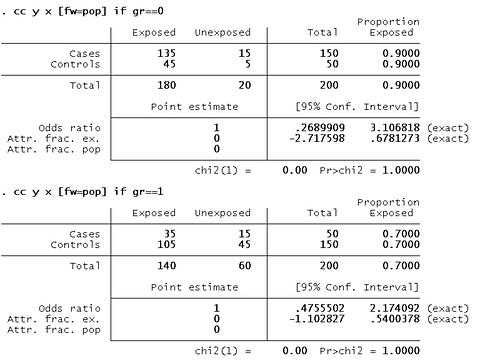
เมือแยกวิเคราะห์แต่ละกลุ่มอายุ odds Ratio เท่ากับ 1 
การอ้วนหรือไม่อ้วนไม่ได้ทำให้การป่วยมากขึ้นหรือน้อยลง

Odds Ratio เปลี่ยนจาก 1.88 เป็น 1 เมื่อ Stratified ด้วยกลุ่มอายุ 
gr_0 ป่วย 150 / 200
gr_1 ป่วย  50 / 200
กลุ่ม gr_0 ป่วยโรค "y" เป็น 3 เท่าของกลุ่ม gr_1

เพื่อให้ STATA วิเคราะห์แบบ Sreatified Analysis คำสังคือ 
cc y x [fw=pop], by (gr)

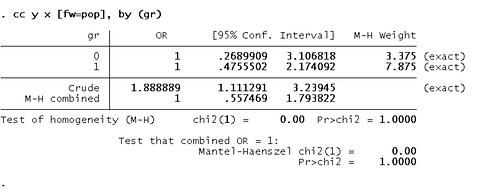
cc y x [fw=pop], by (gr)
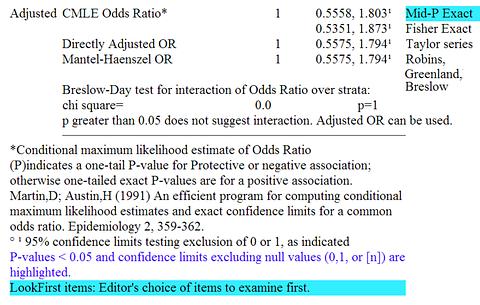
M-H Adjusted Odds Ratio จะได้ค่า Odds Ratio =1
ตรงกันกับการแยกวิเคราะห๋ gr =0 และ gr=1 ซึ่ง Odds Ratio =1
แต่ถ้ารวมกันแบบ crude
จะได้ค่า Odds Ratio = 1.88  เหมือนกันกับการวิเคราะห์ที่ไม่ได้แยกกลุ่มอายุ
ซึ่งได้ค่า Odds Ratio = 1.88  ทำให้เข้าใจว่าการอ้วนเกิดโรค "y" เป็น 1.88 เท่าของการไม่อ้วน

กลุ่มอายุน้อยป่วย โรค "Y"  150 / 200
กลุ่มอายุมากป่วย โรค "Y"    50 / 200
อายุน้อยป่วยโรค "y" มากกว่าอายุมาก 
กลุ่มอายุน้อยป่วยโรค "y" 3 เท่าของกลุ่มอายุมาก

OpenEpi การวิเคราะห์แยกแต่ละกลุ่ม Stratified Analysis
Options/Settings
ให้ Exposure อยู่ด้านบนของ 2x2 Table เหมือนกับ STATA

Adjusted Odds Ratio ทำไม? 
และ Adjusted อย่างไร?
การนำตัวเลข Stratum 1 และ Stratum 2 "รวมกันแบบ Crude" ได้ค่า Odds Ratio =1.88
แต่ถ้าใช้วิธี M-H Adjusted OR คือ Adjusted ด้วยตัวแปรกลุ่มอายุ Odds Ratio = 1 
เหมือนกันกับการ "แยก Crude" Stratified ออกเป็น Stratum 1 และ Stratum 2 
ซึ่งแต่ละ Stratum ได้ Odds Ratio = 1
OR =1.88 การอ้วนเกิด โรค "y" เป็น 1.88 เท่าของการไม่อ้วน
OR = 1 การอ้วนและการไม่อ้วนเกิดโรค "y" เท่าๆ กัน 

Stratum 1	OR = 1
Stratum 2	OR = 1
Crude	OR = 1.88
M-H Adjusted	OR = 1

References
Confounding Factor Criteria จาก blog oknation 
http://www.oknation.net/blog/print.php?id=417153

เพศเป็น Confounder (ข้อมูลสมมุติ) Risk Based
http://www.gotoknow.org/posts/437227

Simpson's paradox (งานวิจัยจาก ncbi)
นิ่วก้อนเล็กวิธี A ดีกว่า 
นิ่วก้อนใหญ่วิธี A ดีกว่า
รวมนิ่วก้อนเล็กและนิ่วก้อนใหญ่วิธี B ดีกว่า ?
http://www.gotoknow.org/posts/439144

http://www.statsdirect.com/help/basics/confounding.htm
http://www.healthknowledge.org.uk/node/803
http://www.collemergencymed.ac.uk/CEM/Research/technical_guide/biasconfound.htm