อสงไขย....Ar song kai ???

     

…. เป็นเรื่องของ.... “การนับเวลา” ของ.... “อสงไขย” ...
 การนับ อสงไขย นั้น จะต้องรู้จักกับคำหลายคำต่อไปนี้

     1. อสงไขยปี
     2. รอบอสงไขยปี
     3. อันตรกัป
     4. อสงไขยกัป
     5. มหากัป

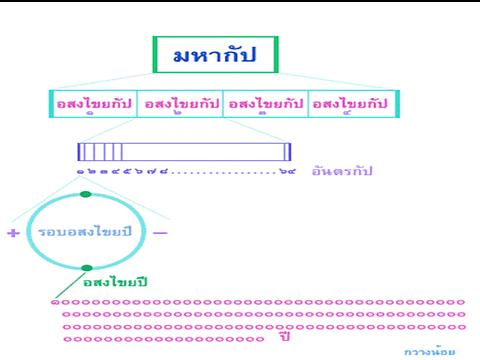
 คำทั้งหมด....มีความหมาย และ...มีความสัมพันธ์กัน....ดังนี้

 1 รอบอสงไขยปี        เป็น 1 อันตรกัป
 64 อันตรกัป              เป็น 1 อสงไขยกัป
 4 อสงไขยกัป            เป็น 1 มหากัป

อสงไขยปี.... เป็นอย่างไร...ในยุคแรกๆ มนุษย์นั้น จะมีอายุขัยที่ยืนยาวมาก คือ....จะมีอายุ เท่ากับ เอาเลข 1 นำหน้า ....แล้ว....ตามด้วยเลข 0 อีก 140 ตัว จำนวนทั้งหมดนี้....เรียกว่า  อสงไขยปี

หนึ่งรอบอสงไขยปี เป็นอย่างไร

.... ในทุก 100 ปี มนุษย์...เราจะมีอายุขัยสั้นลง 1 ปี และ...จะเป็นอยู่อย่างนี้เรื่อยมา คือ จะมีอายุขัยสั้นลงๆจนกว่าจะมี... อายุขัยที่ต่ำสุด คือ 10 ปี .... การลดลงของอายุขัยก็จะหยุดลง และ....จะเริ่มต้น .. การมีอายุที่ยืนยาวขึ้น จาก 10 ปี เป็น 11 ปี .... โดยใช้วิวัฒนาการ...ทุกๆ 100 ปี เช่นกัน และ....จะมีการพัฒนาเช่นนี้ ต่อไปเรื่อยๆ จนกว่า อายุ จะเท่ากับ อสงไขยปี เช่นเดิม ... คือ 1 แล้วตามด้วย 140 ศูนย์ 

กำหนดระยะเวลา....ทั้งหมดนี้ เราเรียกว่า หนึ่งรอบอสงไขยปี และการที่ครบรอบ..หนึ่งอสงไขยปี ... นี้แหละ ก็จะเท่ากับ หนึ่ง อันตรกัป

อสงไขยกัป เป็นอย่างไร

เมื่อนับจำนวน....อันตรกัปตามที่พูดมานั้น ได้ครบ 64 อันตรกัป นั้น จึงเรียกว่า อสงไขยกัป คำว่า อสงไขยกัป

อสงไขยกัป  มีอยู่ 4 อสงไขยกัป ด้วยกัน โดยแบ่งเป็นตอนๆ ดังนี้ คือ

 1. สังวัฏฏอสงไขยกัป เป็นอสงไขยกัป ที่ปรากฏในตอนที่โลกถูกทำลายได้แก่คำว่า สงวฏฏตีต สงวัฏโฏ คือ กัปที่กำลังพินาศอยู่

 2. สังวัฏฏฐายีอสงไขยกัป เป็นอสงไขยกัป ที่ปรากฏในตอนที่โลกถูกทำลายเสร็จเรียบร้อยแล้ว ซึ่งได้แก่คำว่า สงวฏโฏ หุตวา ติฏฐตีติ สงวฏฏฐยี คือ กับที่มีแต่ความพินาศตั้งอยู่

 3. วิวัฏฏอสงไขยกัป เป็นอสงไขยกัป ที่ปรากฏในตอนที่โลกกำลังจะเริ่มพัฒนาเข้าสู่สภาวะปกติซึ่งได้แก่คำว่า วิวฏฏตีติ วิวฏโฏ คือกัปที่กำลังเริ่มเจริญขึ้น

 4. วิวัฏฏฐายีอสงไขยกัป เป็นอสงไขยกัป ที่ปรากฏในตอนที่โลกเจริญขึ้น พัฒนาเรียบร้อยเป็นปกติตามเดิมแล้ว ซึ่งได้แก่คำว่า วิวฏโฏ หุตวา ติฏฐตีติ วิวฏฏฐายี คือกัปที่เจริญขึ้น พร้อมแล้วทุกอย่างตั้งอยู่ตามปกติ

สัตว์โลก ทั้งหลาย เช่น มนุษย์ จะมีชีวิตอยู่ในโลกนี้ได้... ก็เฉพาะตอน อสงไขยกัปสุดท้าย คือ วิวัฏฏฐายีอสงไขยกัป นี้เท่านั้น..... ส่วนในตอน 3 อสงไขยกัป ข้างต้น จะไม่มีสิ่งที่มีชีวิตอาศัยอยู่ในโลกนี้เลย 

มหากัป เป็นอย่างไร

 เมื่อนับ..จำนวนทั้ง 4 อสงไขยรวมกัน เราจะเรียกว่า 1 มหากัป คือ

 1. สังวัฏฏอสงไขยกัป นานถึง 64 อันตรกัป

 2. สังวัฏฏฐายีอสงไขยกัป นานถึง 64 อันตรกัป

 3. วิวัฏฏอสงไขยกัป นานถึง 64 อันตรกัป

 4. วิวัฏฏฐายีอสงไขยกัป นานถึง 64 อันตรกัป

รวม 4 อสงไขยกัป ก็เป็น 256 อันตรกัป ซึ่งจะเท่ากับ 1 มหากัป
แต่ทีนี้เวลาบอกว่า พระพุทธเจ้าได้บำเพ็ญเพียร สั่งสมบารมี เป็น 4 อสงไขย  กับ  หนึ่งแสนมหากัป 

นั้น คำว่า อสงไขย  หมายถึง การนับจำนวนของมหากัป เป็นอสงไขย กับอีก หนึ่ง แสน มหากัป 

คำว่า กัป และ กัล นั้น ต่างก็มีความหมาย...เหมือนกัน ...แตกต่างกัน ที่ คำหนึ่งเป็น ภาษาบาลี อีกคำหนึ่งเป็น ภาษาสันสกฤต 

 แหล่งข้อมูล จากหนังสือชื่อ ศาสตร์ว่าด้วยการเป็นพระพุทธเจ้า (มุนีนาถทีปนี) สำนักพิมพ์ คณะสังคมผาสุก ผู้แต่ง พระเทพมุนี (วิลาส ญาณวโร) ISBN: 974-7437-92-9

....หมอเปิ้น .... ชอบเพลงนี้มากๆๆ ค่ะ .... เนื้อหาดี.... มีความหมายที่ดีค่ะ ...  เรามาฟังเพลง ...นี้กันนะคะ

          เพลง ....อสงไขย ....วง...The sis

     ปล่อยความคิดถึง......ปลิวไปในอากาศ

     ล่องลอยหัวใจสะอาด....ปล่อยไปแสนไกล

     กรุ่นกลิ่นบุหงา.....พัดมาด้วยรักจากใจ

     เพียงหวังให้ถึงใคร......คนที่รอคนนั้น

     ส่งความคิดถึง......ปลิวไปในอากาศ

     คิดถึงใจจะขาด..... เธออาจไม่เข้าใจ

     แค่อยากให้รู้ .....ไม่ได้ต้องการสิ่งใด

     เธอไม่ต้องขืนใจ.....ถ้าเธอไม่ต้องการ

      ฝากเป็นเพลง.....ให้ลอย ....เล่นลมไป 

      ล่องลอย.....ผ่านไปถึงเธอ

      แม้จะเนิ่นนาน.....ยังรักเธอ

      ตราบนาน....อสงไขยเวลา

      หากเพลงคิดถึง.....ที่ปลิวไปในอากาศ

      เพียงถ้ามันพลั้งพลาด....ไปไม่พบเธอ

      ให้บทเพลงนี้ ..... ล่องลอยไปเสมอ

      รอสักวันที่เจอ .... คนที่เขาต้องการ

       ฝากเป็นเพลง ให้ลอยเล่นลมไป

       ล่องลอย ผ่านไปถึงเธอ
       แม้จะเนิ่นนาน ยังรักเธอ 

       ตราบนาน อสงไขยเวลา
       แม้จะเนิ่นนาน ยังรักเธอ 

       ตราบนาน อสงไขยเวลา

        ขอบคุณมากๆนะคะ....

             

             

                         

              

[โสภณ เปียสนิท]

ดูเหมือนจะนานนับกัปป์กัลป์ คือนานเท่าใดครับ

 

[Dr. Ple]

 

  ขอบคุณมากๆๆ นะคะ  พี่ๆๆ น้องๆๆ  มากค่ะ

 

 

	นาย ธนา นนทพุทธ
	อ.นุ
	โสภณ เปียสนิท

 

 

 

[Bright Lily]

คิดถึง " เราจะข้ามเวลามาพบกัน" "แม้ชั่วกับชั่วกัลป์ ก็จะไปพบเธอ"

wording ประทับใจค่ะ

[Dr. Ple]

ขอบคุณมากๆๆนะคะ ท่าน Bright Lily ขอบคุณกับข้อ Comment ดีดี ที่มีให้นะค

ขอบคุณค่ะ

[kunrapee]

นานนนนนนนนนน

แสนนนนนนนนนน

นานนนนนนนนนน

[ยายธี]

..อ้ะ..สง.สัย..น่า..ค่า....ทำมายจึง..นานนน อย่างนั้นนนน...ยยยยายยยธธธธี..เจ้าค่า

[Dr. Ple]

 

ขอบคุณ มากๆๆนะคะ ... พี่  เพื่อนๆๆ  น้องๆๆ มากๆๆนะคะ

 

	kunrapee
	Bright Lily
	Wasawat Deemarn
	นาย ธนา นนทพุทธ
	อ.นุ
	ยายธี
	โสภณ เปียสนิท

           ขอบคุณ ด้วยความจริงใจค่ะ

 

 

[Dr. Ple]

 

 

 

ขอบคุณมาก  น้อง  kunrapee    น่ารัก กับ พี่เปิ้น เสมอมานะคะ น้องสบายดี นะคะ

 

[Dr. Ple]

 

 

 

ขอบคุณ .... ยายธี ที่น่ารักของ .... หมอเปิ้น ...ก็ไม่รู้ว่า...นาน...นานนนนนน อย่างไรนะคะ.. ตำรา ....... เขาว่า อย่างนั้น .....นะคะ คิดถึงนะคะ ...  ยายธีอย่าง มากๆๆ  นะคะ

 

[sr]

Out of curiosity I looked up (but I am none-the-wiser ;-)

asaṃkhaya อสงไขย (asaṃ + khaya) = 10^139

Asa (adj.) [for asaŋ = asanto, a + santo, ppr. of 'as' in meaning "good"] bad J iv.435 = vi.235 (sataŋ vā asaŋ acc. sg. with v. l. santaŋ . . ., expld -- by sappurisaŋ vā asappurisaŋ vā C.); v.448 (n. pl. f. asā expld. by asatiyo lāmikā C.; cp. p. 446 v.319).

khaya: waste; destruction; decay; consummation of. (m.) Kappa (adj. n.) [Sk. kalpa, see kappeti for etym. & formation] anything made with a definite object in view prepared, arranged; or that which is fit, suitable, proper See also DA i.103 & KhA 115 for var. meanings

Googol (10^100) and Googolplex 10^googol

From http://en.wikipedia.org/wiki/Graham%27s_number :

Graham's number is unimaginably larger than other well-known large numbers such as a googol, googolplex, and even larger than Skewes' number and Moser's number. Indeed, the observable universe is far too small to contain an ordinary digital representation of Graham's number, assuming that each digit occupies at least one Planck volume. Even power towers of the form \scriptstyle a ^{ b ^{ c ^{ \cdot ^{ \cdot ^{ \cdot}}}}} [a^(b^(c^d...))] are useless for this purpose, although it can be easily described by recursive formulas using Knuth's up-arrow notation or the equivalent, as was done by Graham. The last ten digits of Graham's number are ...2464195387.

Specific integers known to be far larger than Graham's number have since appeared in many serious mathematical proofs (e.g., in connection with Friedman's various finite forms of Kruskal's theorem). \scriptstyle N \;=\; F^7(12) \;=\; F(F(F(F(F(F(F(12))))))) \,\!, where \scriptstyle F(n) \;=\; 2\uparrow^{n} 3 \,\! in Knuth's up-arrow notation. The lower bound of 6 was later improved to 11 by Geoff Exoo in 2003, and to 13 by Jerome Barkley in 2008. Thus, the best known bounds for N* are 13 ≤ N* ≤ N. Graham's number, G, is much larger than N: \scriptstyle f^{64}(4), where \scriptstyle f(n) \;=\; 3 \uparrow^n 3.

[ปิยะกุล]

เพราะค่ะ