7QC - Histogram

ฮิสโตแกรม (Histogram) 

                คือ กราฟแท่งแบบเฉพาะ โดยแกนตั้งจะเป็นตัวเลขแสดง “ ความถี่ ” และมีแกนนอนเป็นข้อมูลของคุณสมบัติของสิ่งที่เราสนใจ โดยเรียงลำดับจากน้อย ที่ใช้ดูความแปรปรวนของกระบวนการ โดยการสังเกตรูปร่างของฮิสโตแกรมที่สร้างขึ้นจากข้อมูลที่ได้มาโดยการสุ่มตัวอย่าง

                มีประโยชน์ในการที่จะทำให้ทราบถึงการแจกแจงของสิ่งที่เราต้องการวิเคราะห์ ประโยชน์ประการสำคัญของการใช้ฮีสโตแกรม คือการใช้เพื่อวิเคราะห์ความถี่ของข้อมูลแล้วตัดสินใจว่า การแจกแจงหรือการกระจายข้อมูลแบบใด เพื่อใช้ตรวจสอบคุณสมบัติของข้อมูล ตลอดจนการประมาณการลักษณะคุณภาพที่ได้จากการผลิต

           แผนภูมิฮิสโตแกรม แผนภูมินี้จะชี้ให้เห็นถึงความเบี่ยงเบนของข้อมูลว่ามีลักษณะการกระจายตัวของข้อมูลเป็นแบบระฆังคว่ำ (Normal Distribution) หรือไม่ หรือมีความเบี่ยงเบนไปทางบวกหรือลบ หรือมีลักษณะรูปแบบแบบฟันเลื่อย หรือแบบหน้าผา เป็นต้น ทำให้มองเห็นว่าความเบี่ยงเบนที่เกิดขึ้นจาก Normal Distribution ควรจะแก้ไขอย่างไร

เมื่อไรจึงจะใช้แผนภาพฮิสโตแกรม
                •  เมื่อต้องการตรวจสอบความผิดปกติ โดยดูการกระจายของกระบวนการทำงาน
                •  เมื่อต้องการเปรียบเทียบข้อมูลกับเกณฑ์ที่กำหนด หรือค่าสูงสุด-ต่ำสุด
                •  เมื่อต้องการตรวจสอบสมรรถนะของกระบวนการทำงาน (Process Capability)
                •  เมื่อต้องการวิเคราะห์หาสาเหตุรากเหง้าของปัญหา (Root Cause)
                •  เมื่อต้องการติดตามการเปลี่ยนแปลงของกระบวนการในระยะยาว
                •  เมื่อข้อมูลมีจำนวนมากๆ 

วิธีการเขียนฮิสโตแกรม (Histogram)
                •  เก็บรวบรวมข้อมูล (ควรรวบรวมประมาณ 100 ข้อมูล)
                •  หาค่าสูงสุด (L) และค่าต่ำสุด (S) ของข้อมูลทั้งหมด
                •  หาค่าพิสัยของข้อมูล (R-Range)

                                                สูตร R = L - S

                •  หาค่าจำนวนชั้น (K)

                                                สูตร K = Square root of (n) โดย n คือ จำนวนข้อมูลทั้งหมด

                •  หาค่าความกว้างช่วงชั้น (H-Class interval)

                                                สูตร H = R/K หรือ พิสัย / จำนวนชั้น

                •  หาขอบเขตของชั้น (Boundary Value)

                                                ขีดจำกัดล่างของชั้นแรก = S – หน่วยของการวัด / 2

                                                ขีดจำกัดบนของชั้นแรก = ขีดจำกัดล่างชั้นแรก + H

                •  หาขีดจำกัดล่างและขีดจำกัดบนของชั้นถัดไป

                •  หาค่ากึ่งกลางของแต่ละชั้น (Median of class interval)

                                                ค่ากึ่งกลางชั้นแรก = ผลรวมค่าขีดจำกัดชั้นแรก / 2

                                                ค่ากึ่งกลางชั้นสอง = ผลรวมค่าขีดจำกัดชั้นสอง / 2

                •  บันทึกข้อมูลในรูปตารางแสดงความถี่
                •  สร้างกราฟฮิสโตแกรม

ลักษณะต่างๆ ของฮิสโตแกรม
•  แบบปกติ (Normal Distribution)   

   การกระจายของการผลิตเป็นไปตามปกติ ค่าเฉลี่ยส่วนใหญ่จะอยู่ตรงกลาง

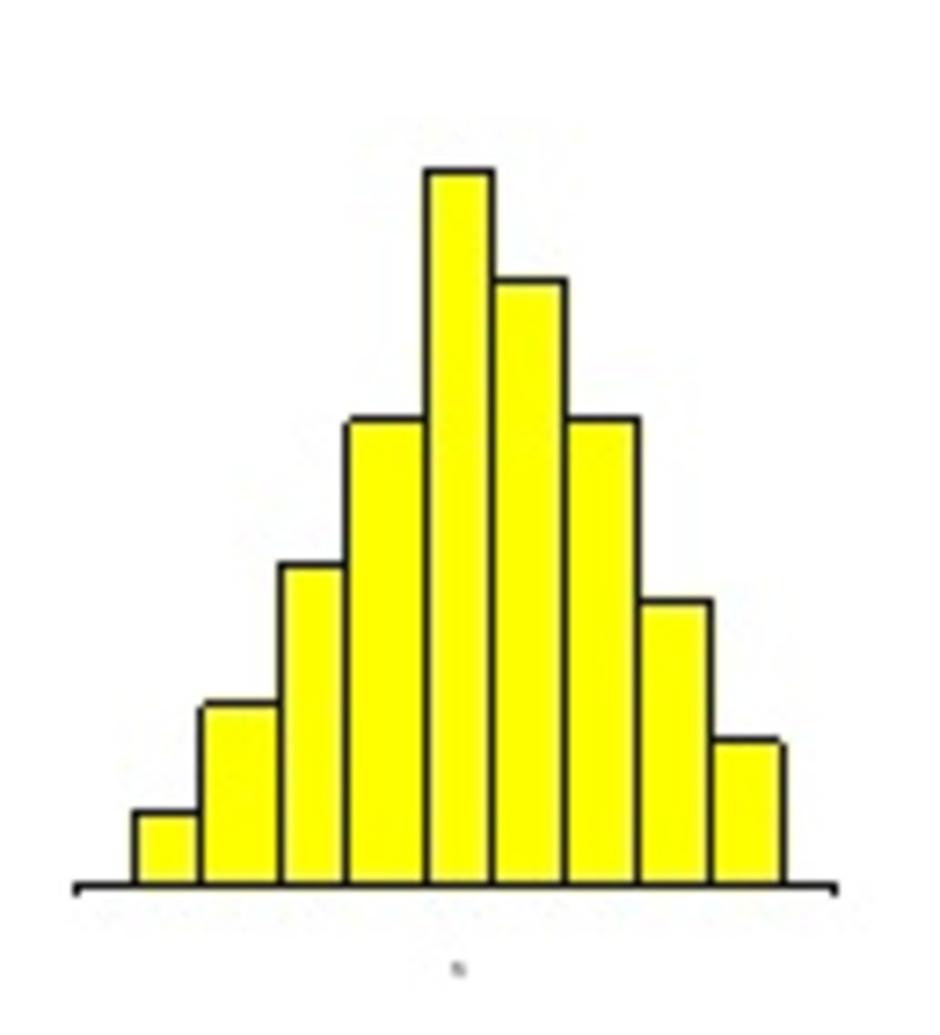
•  แบบแยกเป็นเกาะ (Detached Island Type)    

    พบเมื่อกระบวนการผลิตขาดการปรับปรุง/หรือการผลิตไม่ได้ผล

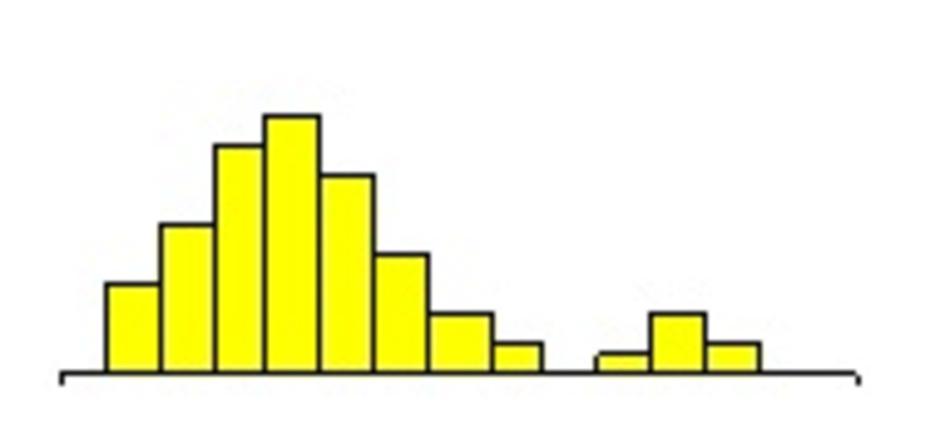
•  แบบระฆังคู่ (Double Hump Type)  

    พบเมื่อนำผลิตภัณฑ์ของเครื่องจักร 2 เครื่อง / 2 แบบมารวมกัน

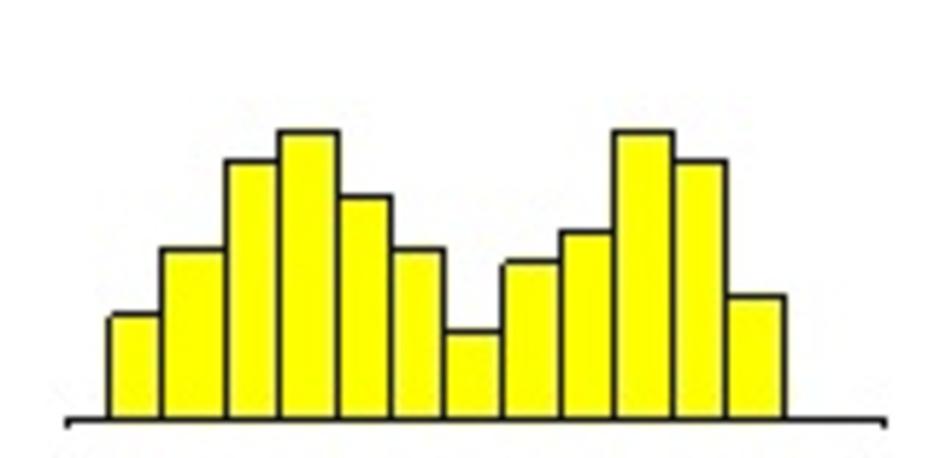
•  แบบฟันปลา (Serrated Type)  

   พบเมื่อเครื่องมือวัดมีคุณภาพต่ำ หรือการอ่านค่ามีความแตกต่างกันไป

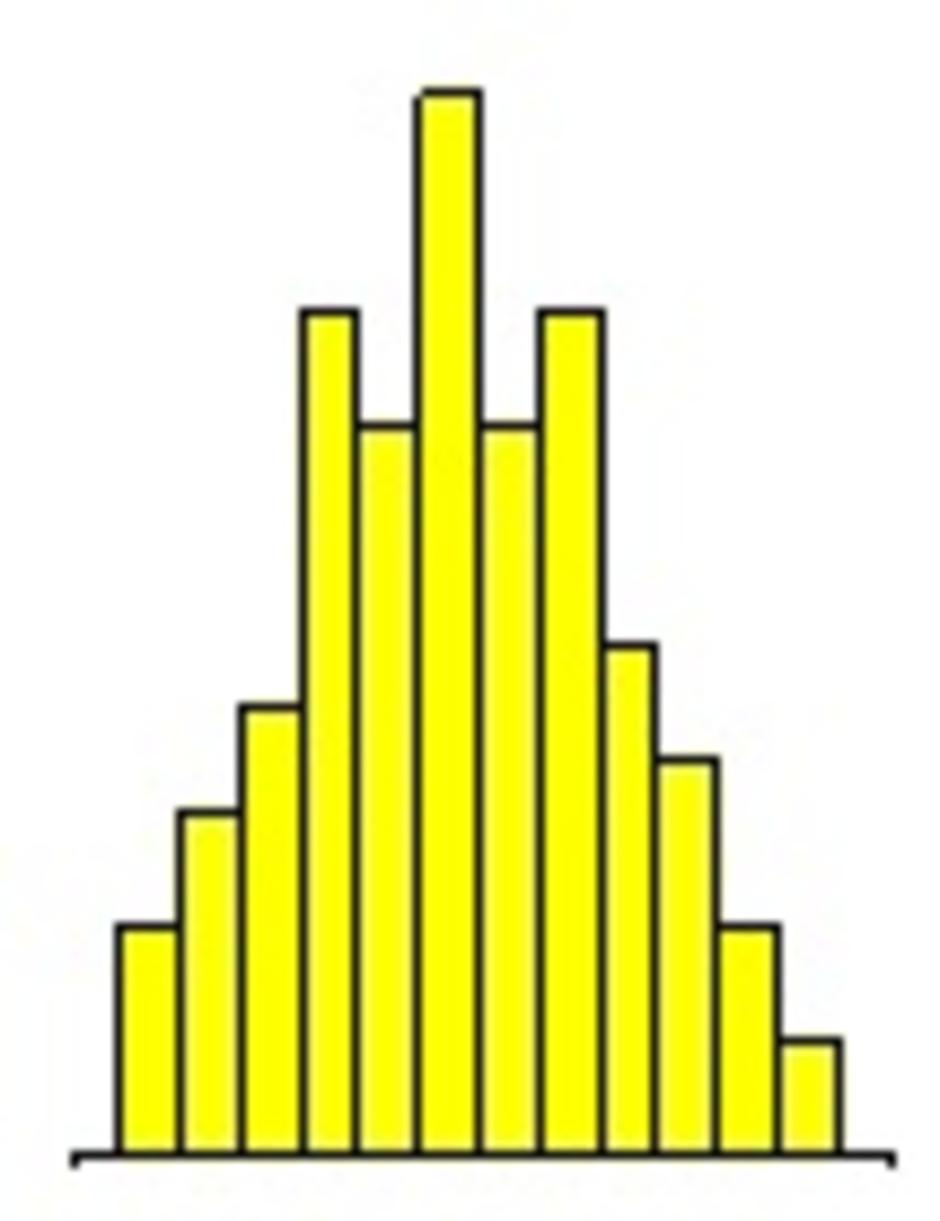
•  แบบหน้าผา (Cliff Type)   

    พบเมื่อมีการตรวจสอบแบบ Total Inspection เพื่อคัดของเสียออกไป