ธรรมชาติกับคณิตศาสตร์ ... จากฟิโบนักชีสู่โครงสร้างทางชีววิทยา
สวัสดีครับทุกคนที่รักธรรมชาติ
สบายดีกันนะครับ เมื่อวาน (18.เมษายน 2551) โปรเฟสเซอร์วิลลี่ เยเกอร์ ท่านได้พูดในสัมมนาเรื่อง
Kann die Natur Mathematik? แปลตรงๆ เป็นอังกฤษจะได้ว่า Can nature Mathematics?
มีจำนวนผู้เข้าฟังสัมมนาเต็มห้องเลยครับ ตั้งแต่น้องๆ ระดับมัธยมศึกษา ไปจนถึง นักศึกษาในมหาวิทยาลัย ระดับต่างๆ จนถึงโปรเฟสเซอร์อีกหลายๆ คนเข้าร่วมฟังครับ เวลาผมเห็นบรรยากาศแบบนี้นะครับ ทำให้ผมนึกถึงอยากให้มีบรรยากาศแบบนี้ในประเทศไทย บ้านเรามากๆ เลยครับ



(From http://www.ph-heidelberg.de/wp/filler/mathabend/matheabend1.html)
ผมจึงขอนำแนวคิดเกี่ยวกับธรรมชาติกับคณิตศาสตร์มาฝากนะครับ ว่าด้วยเรื่องของจากลำัดับฟิโบนักชี Fibonacci sequence มาสู่ธรรมชาติดูนะครับ จริงๆ ว่าไปก็คือ ลำดับเลขฟิโบนักชีก็ได้จากการสังเกตของนักคณิตศาสตร์ชาวอิตาเลียนชื่อ เลโอนาร์โด ฟีโบนักชี (Leonardo Fibonacci) แห่งเมื่องปิซา ในสมัย ค.ศ. 1202 นะครับ ได้สังเกตจำนวนคู่ของกระต่าย
โดยมีข้อมูลดังนี้คือ
เดือนที่ 1 มีลูกกระต่าย 1 คู่
เดือนที่ 2 มีลูกกระต่าย 1 คู่
เดือนที่ 3 มีลูกกระต่าย 2 คู่
เดือนที่ 4 มีลูกกระต่าย 3 คู่
เดือนที่ 5 มีลูกกระต่าย 5 คู่
เดือนที่ 6 มีลูกกระต่าย 8 คู่
เดือนที่ 7 มีลูกกระต่าย 13 คู่
เดือนที่ 8 มีลูกกระต่าย 21 คู่
เดือนที่ 9 มีลูกกระต่าย 34 คู่
ไปเรื่อยๆ โดยมีความสัมพันธ์ว่า
จำนวนกระต่ายในเดือน นั้น มีจำนวนคู่ เ่ท่ากับจำนวนกระต่ายในสองเดือนก่อนนั้น รวมกัน
เช่น กระต่ายในเดือนที่ 10 เท่ากับจำนวนกระต่ายในเดือนที่ 9 รวมกับ เดือนที่ 8 ซึ่งมีจำนวน 55 คู่นั่นเอง
เราจึงนำจำนวนคู่ของกระต่ายมาเรียงต่อกันเป็นลำดับ ดังนี้
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, .... ไปเรื่อยๆ
และเราเรียกลำดับชุดตัวเลขนี้ว่า ลำดับฟิโบนักชี นั่นเองครับ

(ภาพจาก ... http://britton.disted.camosun.bc.ca/fibslide/fib00.jpg )
ผมจะยกตัวอย่างหนึ่ง เกี่ยวกับ ดอกไม้ก็แล้วกันนะครับ ทุกคนก็เคยชินและคุ้นกับการนับกลีบดอกไ้ม้อยู่แล้วนะครับนะครับ เช่น ที่เราเล่นกันว่า รัก ไ่ม่รัก รัก ไม่รัก นับไปเรื่อยๆ จนกว่าจะหมดกลีบครับ...ซึ่งโดยส่วนใหญ่เรากำหนดได้่ว่าจะให้ลงท้ายด้วยคำว่า รักหรือ ไม่รัก หากเรารู้ว่า จำนวนกลีบของดอกไม้นั้นๆ ว่ามีกี่กลีบนะครับ
มาดูกันเลยนะครับ
- จำนวน หนึ่งกลีบ เช่น white calla lily

- จำนวน 2 กลีบ เช่น euphorbia

- จำนวน 3 กลีบ เช่น trillium

- จำนวน 5 กลีบ เช่น columbine

- จำนวน 8 กลีบ เช่น bloodroot

- จำนวน 13 กลีบ เช่น black-eyed susan

- จำนวน 21 กลีบ เช่น shasta daisy

- จำนวน 34 กลีบ เช่น field daisies

เห็นไหมครับ ว่าดอกไม้ส่วนใหญ่จะีมีจำนวนกลีบเท่ากับจำนวนค่าตัวเลขค่าใดค่าหนึ่ง เป็นส่วนใหญ่ครับ แต่ก็มีดอกไม้จำนวนหนึ่งนะครับ ที่ไม่เป็นไปตามหลักนี้ครับ เช่น มี จำนวน 4 กลีบ หรือ 6 กลีบ หรือ 10 ดอก ครับ
นี่คือตัวอย่างที่ อยู่นอกเหนือกฏจากลำดับนี้นะครับ กรณีที่เป็นดอกไม้นะครับ

This flower (prairie blue-eyed grass) has six petals. มี 6
กลีบ
Credit: I. Peterson (from http://www.maa.org/mathland/mathtrek_06_05_06.html)

A flower with 10 petals. มี 10 กลีบ
Credit: I. Peterson (from http://www.maa.org/mathland/mathtrek_06_05_06.html)
คราวนี้ เรามาลองพิจารณากรณีที่เป็นต้นไ้ม้ดูบ้างนะครับ

จากภาพต้นไม้ตัวอย่างนี้นะครับ หากเราแบ่งเป็นระดับชั้นๆ ดังต่อไปนี้นะครับ

คุณลองนับดูไหมครับ นับจำนวนกิ่งดูไหมครับ ว่าในแต่ละชั้นได้จำนวนกิ่งกี่กิ่งครับ

เห็นไหมครับ ว่าจะได้ตัวเลข เป็นชุดในลำดับของ ฟิโบนักชีเลยครับ แล้วหากเรานับจำนวนใบดูละครับ

จำนวนใบก็เป็นไปตามนั้นเช่นกันนะครับ แต่นี่อาจจะเป็นจำนวนพืชเพียงจำนวนหนึ่งครับที่เป็นไปตามแบบนี้ครับ

มาดูอีกกรณีนะครับ การนับจำนวนกิ่งและลำต้นนะครับ

ต่อไปมาลองดูอีกตัวอย่างนะครับ เกี่ยวกับการจัดเรียงใบ ของใบไม้นะครับ ตามหลักแล้วธรรมชาติได้ออกแบบมาอย่างชาญฉลาดมากๆ นะครับ ใบไม้มักจะมีการจัดเรียงใบเพื่อรับแสง
หากคุณเคยสังเกตต้นไม้ ใบไม้ เราจะเห็นการจัดเรียงของใบไม้ มาลองดูโมเดลจำลองการจัดเรียงของใบไม้จากใบล่างสุดไปยังใบสูงสุดครับ

สิ่งที่เราจะพิจารณาได้คือ จากใบล่างสุด แล้วก็ให้นับจำนวนใบวนทวนเข็มนาฬิกาโดยนับค่าสองค่าดังต่อไปนี้คือ
- จำนวนใบ (Leaves)
- จำนวนรอบ (Revolutions)
ความหมายก็คือว่า ให้สังเกตใบที่เรายึดล่างสุด จะอยู่ตรงกับอีกใบหนึ่งในชั้นบน นั่นคือ จำนวนใบในการครบกี่รอบ นั่นเอง ยกตัวอย่างเช่น
เรานับได้ ว่า มีจำนวน 2 รอบ มีจำนวน 5 ใบ เราจะได้อัตราส่วนที่เรียกว่า Phyllotaxis ครับ
โดยค่านี้ จะมีค่าทำกับ = จำนวนรอบ ต่อ จำนวนใบที่มี = 2/3 นั่นเอง

เราลองมานับดูนะครับ ว่าวิธีการจัดเรียงใบของต้นใบอย่างชาญฉลาดเพื่อเพิ่มพื้นที่การรับแสงในการนำไปสังเคราะห์อาหารในการเลี้ยงอุ้มชูลำต้นนะครับ

ภาพจาก http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibnat.html
ค่านี้จะเป็นค่าการจัดเรียงใบของพืชนั้นๆ นั่นเองครับ พืชแต่ละชนิดจะมีค่านี้ต่างๆ กันไปครับ แต่ในพันธุ์เดียวกันจะมีการเรียงเหมือนกัน เช่น 1/2, 3/5, 3/8, 5/8, ....
ในตัวเลขในลำดับฟิโบนักชี ยังสามารถจะอธิบายการจัดเรียงเมล็ดของทานตะวันได้อีกเช่นกันครับ หรือการจัดเรียงของตาสับปะรด ดังเช่นภาพต่อไปนี้ครับ

และสำหรับ สับปะรด

ว่างๆ มีโอกาสซื้อหรือเจอสิ่งเหล่านี้ลองนับๆ กันดูนะครับ เป็นคณิตศาสตร์ในธรรมชาติ ที่อยู่ใกล้ตัวเรานั่นเองครับ
คราวนี้....หากเรากลับไปดูลำดับฟิโบนักชีกันอีกรอบนะครับ
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, .... ไปเรื่อยๆ
หากเรานำค่าสองค่าที่อยู่ติดกันมาหารกัน โดยเอาตัวหน้าตั้งและตัวที่ตามมาเป็นตัวหาร เราจะได้ว่า
1/1, 1/2, 2/3, 3/5, 5/8, 8/13, 13/21, 21/34, 34/55, 55/89, ... ไปเรื่อยๆ
เราจะเรียกค่าอัตราส่วนนี้ว่า อัตราส่วนทอง Golden Ratio นั่นเองครับ ซึ่งค่านี้ จะมีความสำคัญในการอธิบายและออกแบบของธรรมชาติมากๆ นักออกแบบทั้งหลายจึงนิยมใช้ อัตราส่วนทองและตัวเลขฟิโบนักชีในการนำไปประยุกต์ใช้จนอย่างแพร่หลายในปัจจุบัน
เห็นไหมครับ ว่าในธรรมชาิตินั้น มีอะไรใกล้ๆ ตัวเรามากมาย แม้แต่ตัวเราก็มีตัวเลขและอัตราส่วนทองอีกมากมายเลยนะครับ ผมจะนำเสนอในตอนต่อๆ ไปนะครับ





- ปุ่มของลูกสน
- เมล็ดดอกทานตะวัน มีการจัดเรียงตัวเป็นเกลียวที่หมุนตามเข็มนาฬิกา และทวนเข็มนาฬิกา
- อัตราส่วนระหว่างเส้นผ่านศูนย์กลางของเกลียวเปลือกหอยนอติลุส
- เกลียวการหมุนของยอดปุ่มของกะหล่ำดอกพันธุ์โรมาเนตโก (Romanesco)
- ความยาวของกระดูกนิ้วมือแต่ละข้อจะมีอัตราส่วนเรียงตามลำดับเลขฟีโบนักช
(From http://learners.in.th/blog/eva/55052 )
คุณไปฟังเพิ่มเติมได้จากที่นี่ด้วยนะครับ... น่าสนใจ เป็นการบอกว่าเราพบจากที่ไหนอีกบ้างครับ ในตัวอย่างจากคลิปข้างล่างนี้ จะบอกและยกตัวอย่างมากมายจากธรรมชาตินะครับ
จาก http://www.youtube.com/watch?v=P10wGxupVcY
และตัวอย่างอื่นๆ เช่น
- การไหลของน้ำลงในอ่างล้างจาน
- การหมุนของพายุไต้ฝุ่น
- การงอนของเขาสัตว์
- การขดของลายนิ้วมือก้นหอยของคน
- ระยะต่างๆ ของคนเรา ทั้งภายในภายนอก
- และอื่นๆ อีกมากมายครับ
ข้อมูลอ้างอิงจาก...
- http://britton.disted.camosun.bc.ca/fibslide/jbfibslide.htm
-
http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibnat.html
สำหรับการที่มนุษย์จะนำตัวเลขนี้ไปใช้ ผมจะทยอยเขียนให้อ่านกันนะครับ... เพราะมีบทบาทในการนำไปใช้ในด้านต่างๆ เช่น
- การสร้างบ้าน ปราสาท
และทางการก่อสร้างในด้านวิศวกรรมและสถาปัตย์
- การออกแบบบัตรต่างๆ เช่น บัตรเอทีเอ็ม และบัตรต่างๆ จะเป็นบัตรที่เรียกว่า สี่เหลี่ยมฟิโบนักชี
- การออกแบบรถยนต์ในชิ้นส่วนต่างๆ
-
อื่นๆ อีกมากครับ... เพราะเราพบตัวเลขเหล่านี้จากธรรมชาติ ดังนั้นสิ่งที่มนุษย์สร้างขึ้นก็จะนำมาจากธรรมชาติด้วยนะครับ เพราะเราเชื่อว่าสิ่งเหล่านั้น ธรรมชาติเลือกดีที่สุดแล้ว การที่เราสร้างของใหม่ๆ ขึ้นมาก็นำมาใช้เพื่อให้กลมกลืนกับธรรมชาติด้วยครับ... นี่คือ
จากความงามของธรรมชาติ
สู่
ความงามของคณิตศาสตร์
The
beauty of Mathematics from Nature
ขอบพระคุณมากนะครับ
เม้ง
ความเห็น (38)
สวัสดีครับ
เคยสังเกตดอกทานตะวันมาบ้างเหมือนกันครับ
แต่สับปะรดไม่เคยสังเกต
ผมว่าขนุนกับทุเรียนก็น่าสนใจ อิๆๆ
เรื่องคณิตศาสตร์อยู่ใกล้ตัวนะครับ
ได้แง่ ได้คิดครับ
น่าคิด น่าสนใจมากๆ
มนุษย์นำระบบตัวเลขนี้ไปทำอะไรมาบ้างหรือเปล่าครับ..น้องเม้ง อยากรู้
ตอนเรียนมีเพื่อนนำเสนอเรื่องนี้อยู่เหมือนกันค่ะ
เห็นเขาว่าสถาปัตยกรรมสิ่งก่อสร้างหลายแห่งในยุโรปก็ใช้ประโยชน์จาก Golden Ratio ในการสร้างเช่นกันค่ะ
แต่ก็มีบางกรณีที่ดอกไม้มี 6 กลีบนะ แบบว่าชอบนั่งนับว่าเป็นไปตามฟิโบนาชีทุกกรณีหรือเปล่า
สวัสดีครับคุณธ.วั ช ชั ย
สบายดีนะครับ ขอบคุณมากๆ เลยนะครับ ลองนับๆ ดูนะครับ สำหรับดอกทานตะวันนั้น เราจะนับจำนวนแถวที่โค้งที่เรียกว่า Fibonacci Spiral จากแนวทิศตามเข็มและทิศทวนเข็มนาฬิกาครับ
เราจะได้ว่า จำนวนแถวเหล่านั้นจะเป็น สมาชิกในลำดับของ Fibonacci นั่นเอง ลองทดลองกับขนุนและทุเรียน ดูไหมครับ คิดว่าจะทำเนองเดียวกันครับ
จำนวนกลีบของขั้วมังคุดล่ะครับ ว่ามีกี่ชุดครับ 3 หรือ 5 ครับ
น่าสนใจทั้งนั้นเลยครับ พอเราได้ตัวเลขเหล่านี้จะได้ความสัมพันธ์ จะนำค่าเหล่านี้ไปประยุกต์ใช้ในการทำหรือออกแบบบางอย่างได้ครับ ไม่ว่าจะอยู่ในรูปของน้ำหนัก หรือความกว้างความยาว ความสูง ครับ

อันนี้ ทวนเข็ม มี 21 ตามเข็มมี 34 เป็นจริงเสมอไปหรือไม่ครับ ว่าจำนวนแถวเหล่านี้ จะคือค่าที่อยู่ติดกันในคู่ใดๆ และทิศตามเข็มจะมีค่ามากกว่าทิศทวนเข็ม??????
ขอบคุณมากๆ นะครับ
สวัสดีครับเพื่อนจารุวัจน์
สบายดีนะครับ หากเราโยงไปถึงจำนวนคนที่เกิดขึ้นในครั้งแรก หรือที่บอกกันว่า พระเ้จ้าสร้างคนมา ทำให้ผมนึกถึงการเพิ่มขึ้นของประชากรของคน ว่าจะเป็นไปตาม ลำดับของฟิโบนักชีหรือไ่ม่ครับ
่น่าสนใจนะครับ นี่คือธรรมชาติ
ขอบคุณมากครับ
สวัสดีครับพี่บางทราย (คนเข็นครก ขึ้นภูเขา)
สบายดีไหมครับ เรื่องการนำไปใช้นั้นมีเยอะมากๆ เลยนะครับ ยกตัวอย่างง่ายๆ หากเราจะทำเครื่องร่อนสักเครื่อง...เราคงจะสร้างสุ่มสี่สุ่มห้าไม่ได้ครับ อาจจะศึกษาโครงสร้างของนกครับ
ถ้าไปศึกษาโครงสร้างของนกนะครับ พี่จะพบเรื่องอัตราส่วนทองอย่างแน่นอนครับ ว่าแต่ละช่วงของท่อนปีกนั้น เกี่ยวข้องสัมพันธ์กันอย่างไร
แล้วจึงนำอัตราส่วนเหล่านั้นมาประยุกต์ใช้ครับ และผสมกับกลไกต่างๆ เพื่อสร้างความสมดุลระบบสิ่งที่สร้างขึ้นมาใหม่ครับ
ลองๆ สังเกตดูนะครับ ไม่แน่นะครับ ว่าผืนที่นา ที่ป่าอาจจะมีโครงสร้างเกี่ยวข้องกับสิ่งเหล่านี้ด้วยก็ได้ครับหรือว่า การคดเคี้ยวของลำน้ำด้วยนะครับ เพราะแม้แต่โครงสร้างของใยโปรตีนก็ยังเกี่ยวข้องกับตัวเลขเหล่านี้ด้วยครับ เป็นการนำไปสู่ในเรื่องของการประหยัดและใช้ัทรัพยากรที่คุ้มค่าครับ
พี่เคยสังเกตไหมครับ ว่าต้นไม้ที่แตกกิ่ง จากพื้นดิน ไปยังกิ่งที่แตกกิ่งย่อย เทียบกับความสูงทั้งหมด หรือความสูงที่เหลือจากกิ่งแรกไปยังยอดสุด ว่าเป็นอัตราส่วนกันหรือไม่ ทำไมธรรมชาติสร้างมาแบบนี้ มีผลต่อการดูดน้ำ ลำเลียงอาหารไปยังส่วนต่างๆ ได้ดีที่สุดหรือไ่ม่ครับ?? สิ่งเหล่านี้ คือความงามของธรรมชาติ
ลองวัดอัตราส่วนจากสะดือไปถึงเท้าและสะดือไปถึงหัวของเราแล้วลองมาศึกษาดูไหนครับ ว่ามีค่าอะไรใกล้เีคียงกันบ้างครับ แล้วความยาวของลำไ้ส้เราเชื่อมโยงกับอะไร ทำไมต้องยาวประมาณนั้น ความยาวของลำไ้ส้ใหญ่และลำไส้เล็ก มีอัตราส่วนทองของกันและกันไหมครับ???
อิๆๆๆๆ ชวนคิดนะครับ จินตนาการไม่มีกรอบ...ใช่ไหมครับ
ขอบคุณมากๆนะครับ
สวัสดีครับคุณtar_ISM9
ใช่ครับ มีการนำมาใช้ในการออกแบบอาคารและสถาปัตย์หลายๆ ที่เลยครับ ในยุโรปครับ
สำหรับดอกไม้นั้น ที่ไม่เป็นไปตามกฏก็มีนะครับ แต่เป็นเพียงส่วนน้อยเ่ท่านั้นครับ ผมกำลังคิดว่า ไม่ว่าจะมี 4 กลีบ 6 กลีบ หรือ 10 กลีบ
ก็มีที่มาจาก Fibonacci เช่นกันนะครับ เดี๋ยวผมจะพิสูจน์ให้ดูกันสดๆ นะครับ
จากลำดับ ฟิโบนักชี นี้ครับ
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, .... ไปเรื่อยๆ
ปกติ คนคิดเค้านำจำนวนสองจำนวนที่อยู่ติดกัน รวมกันจะได้จำนวนถัดไปใช่ไหมครับ
คราวนี้ ผมจะสร้างชุดจำนวนใหม่เพื่อไปชดเชยกับจำนวนชุดของกลีบดอกไม้ที่ไม่สอดรับ ให้สอดรับดังนี้นะครับ
โดยทำดังนี้ครับ
- ให้นำเลขทั้ง 3 ตัวที่อยู่ติดกัน รวมกัน แล้วสร้างเป็นลำดับใหม่จะได้ว่า
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ....
ได้ว่า
1+1+2 = 4
1+2+3 = 6
2+3+5 = 10
3+5+8 = 16
5+8+13 = 26
8+13+21 = 42
ต่อไปเรื่อยๆ
ดังนั้น เราจะได้ลำดับต่อไป เป็น
4, 6, 10, 16, 26, 42, .... ไปเรื่อยๆ ลำดับนี้ อาจจะเรียกว่า
Fibonacci-Chuai-Aree Sequence ห้าๆๆๆๆๆๆๆ (ล้อเล่นครับ)
แล้วคุณจะเห็นความงามต่อไปว่า.... เลขสามตัวรวมกันนี้ จะเป็น Fibonacci ของกันและกันด้วย ตามหลักการดั้งเดิมของ ฟิโบนักชี (สองตัวรวมกันได้ตัวถัดไป)
4, 6, 10, 16, 26, 42, 68, 110,.... เห็นไหมครับ ว่านี่เราได้ลำดับใหม่ขึ้นมาอีกแล้วนะครับ
และผมเชื่อเหลือเกินว่า จะมีดอกไ้ม้บางชนิดมีจำนวนกลีบเท่ากับ 16, หรือ 26 กลีบเช่นกัน...
คราวนี้ผมเพิ่มอีกชุดนะครับ คือ การนำจำนวน 4 ตัวจากฟิโบนักชี ดั้งเดิม มารวมกันนะครับ ผมจะได้ว่า
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ....
ได้ว่า
1+1+2+3 = 7
1+2+3+5 = 11
2+3+5+8 = 18
3+5+8+13 = 29
และต่อๆ ไปครับ คุณก็จะได้ลำดับใหม่อีกครับเป็น
7, 11, 18, 29, 47,.... ไปเรื่อยๆ นะครับ และเป็นไปตามกฏดั้งเดิมในการรวมกันของสองจำนวนได้จำนวนถัดไปเช่นกันครับ
และจะเป็นจริงๆ ตลอดไป ไม่ว่าจะเอาจำนวนที่อยู่ติดกันมารวมกันนะครับ...............
หากเราเอาจำนวน สองจำนวนนี้ มาหาอัตราส่วน อาจจะได้อัตราส่วนที่เป็นอัตราส่วนพิเศษและแสดงความงามต่อกันได้อีกต่อไปครับ....
อาจจะเรียกอัตราส่วนนี้ใหม่ได้เป็นอะไรบางอย่าง....ครับ หรือไ่ม่ก็มีคนคิดไว้หมดแล้วครับ....
เห็นไหมครับ...จากกฏง่ายๆ เราก็นำไปใช้ได้ ต่อยอดไปเรื่อยๆ นะครับ
ขอบคุณมากๆ นะครับ
เห็นไหมครับ...ว่า
จากลำดับ ฟิโบนักชี นี้ครับ
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, .... ไปเรื่อยๆ
ไปสู่ลำดับ Fibonacci-Chuai-Aree Sequence (เรียกสนุกๆ หน่อยนะครับ)
ผมขอเรียกเป็นทางการว่า Second-order Fibonacci Sequence โดยมีลำดับดังนี้
4, 6, 10, 16, 26, 42, 68, 110,.... ไปเรื่อยๆ
เราจะอธิบาย ดอกไ้ม้ ที่มีกลีบเช่นดอกต่อไปนี้

This flower (prairie blue-eyed grass) has six
petals. มี 6 กลีบ
Credit: I. Peterson (from http://www.maa.org/mathland/mathtrek_06_05_06.html)

A flower with 10 petals. มี 10 กลีบ
Credit: I.
Peterson (from http://www.maa.org/mathland/mathtrek_06_05_06.html)
ต่อมา...ผมจะขอเรียก ลำดับอีกชุดนะครับ (ได้จากการรวมของ 4 จำนวนเข้าด้วยกัน) อย่างเป็นทางการว่า Third-order Fibonacci Sequence โดยมีลำดับดังนี้
7, 11, 18, 29, 47,.... ไปเรื่อยๆ
โดยค่าในลำดับใหม่นี้จะสนับสนุนจากธรรมชาติดังนี้คือ

Here is a succulent with a clear arrangement of 4 spirals
in one direction
and 7 in the other (ชุดนี้ จะมีลำดับที่ มีจำนวน 4 รอบและ 7 รอบ)
โดยที่เลข
4 อยู่ใน Second-order Fibonacci Sequence
และ 7 อยู่ใน Third-order Fibonacci Sequence
ผมมีอีกสองตัวอย่างนะครับ ที่อยู่ใน Third-order Fibonacci Sequence
ได้แก่

and here is another with 11 and 18 spirals:
11, และ 18 อยู่ใน ลำดับของ Third-order Fibonacci Sequence
และ

whereas this Echinocactus Grusonii Inermis
has 29 ribs
มีค่า 29 อยู่ใน ลำดับของ Third-order Fibonacci Sequence
เห็นไหมครับ ว่า...ท้ายที่สุดแล้ว ทุกอย่างก็เชื่อมกันอย่างสวยงามมากๆ เลยนะครับ......
16 กลีบ...อยู่ในชุดของ Second-order Fibonacci Sequence
ดอกเชอรี่... จาก http://www.isjp.org/Expert/Cherry_Blossoms/CB.html
26 กลีบ...อยู่ในชุดของ Second-order Fibonacci Sequence

จาก http://www.rdrop.com/~paul/main_april2003.html
11 กลีบ...อยู่ในชุดของ Third-order Fibonacci Sequence

จาก http://www.ces.ncsu.edu/depts/hort/consumer/factsheets/roses/chuckles.htm
ต้น Clover ที่เราบอกว่าเป็นต้นนำโชคหากใครพบเจอ ใบที่มี 4 ใบนะครัีบ หรือใครพบ หกใบ เพราะถือว่าจะพบเจอได้น้อยมากกว่า จำนวน 3 ใบ นะครัีบ

ถามว่าทำไมต้น Clover ต้องมีจำนวนใบ 3 ใบ???
นั่นคือ หากทำการเก็บข้อมูล เราจะพบว่าต้นนี้ จะมีใบส่วนใหญ่ 3 ใบ
ส่วน 4 ใบนั้นจะเป็นเพียงจำนวนนั้น ก็ถือว่าโชคดีหากได้เจอ
เหมือนกันเราไปเจอ ปลาช่อน ในบ่อเลี้ยงปลาดุก นะครับ??? อิๆๆ เกี่ยวกันไหมเนี่ยครัีบ????
ตามเข้ามาอึ้งๆๆๆๆๆ น่าสงสารเมืองไทย.......อิอิๆๆ
We have a lot of clover in our yard and I like to look for special ones. I’ve found several four-leaf clovers and even a few five-leaf clovers, but today I found a six-leaf clover. Here’s a picture of it:

Maybe some day someone might find a seven-leaf clover!
from... http://naturenotebook.net/2007/08/
คุณจะเจอใบพิเศษเหล่านี้ด้วยความโชคดีครัีบ เพราะนานๆ กว่าจะพบสักใบครัีบ very rare ฝรั่งบอกอย่างนั้น วันก่อนผมเดินหากดูยากมากๆ ครับ
สวัสดีครัีบพี่บ่าวขจิต ฝอยทอง
สบายดีนะครับ ไม่ได้เข้าไปทักพี่เสียนานเลยครับ อิๆๆ น่าสงสารเมืองไทยใช่ไหมครับ... ทำกันต่อไปครับพี่ ทำเท่านั้น สร้างปัญญาโดยการหาความรู้เพื่อจะได้ทำอย่างมั่นคงครับ
ปัญหาอยู่ที่ใด คำตอบอยู่ที่นั่น....
ขอบคุณมากครับ
สวัสดีค่ะน้องเม้ง
ไม่ได้คุยกันทางนี้นานเลยเนอะ ต่างคนต่างยุ่งมั่ง
เป็นสิ่งที่น่าสนใจมากค่ะ เพราะโดยปกติเรามักไม่ค่อยคิดเรื่องชีววิทยากับคณิตศาสตร์ เพราะคิดว่าคณิตศาสตร์เป็นกายภาพอะไรประมาณนี้แบบต่างคนต่างอยู่ไม่บูรณาการกัน จริงๆแล้วทุกอย่างเกี่ยวข้องกันหมด แต่เรามาจับแยกศึกษาลงลึกไปเฉพาะด้านใดด้านหนึ่ง ทั้งๆที่ต้องบูรณาการ
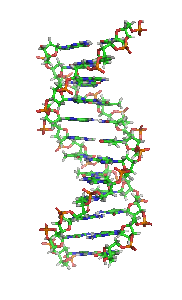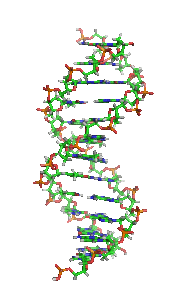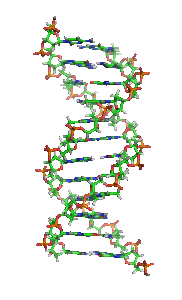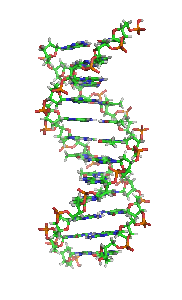
จำนวนต่างๆของสิ่งมีชีวิตเหล่านี้ น่าจะมีจุดเริ่มต้นที่เกี่ยวข้องกับตัวเลขทางคณิตศาสตร์ที่ควบคุมตั้งแต่ในระดับ gene หรือ DNA มั้ยค่ะ ถ้าจำไม่ผิดคนที่ค้นพบ DNA ก็คือ นักฟิสิกส์ ... น้องเม้งช่วยแจกแจงคณิตศาสตร์ตั้งแต่ระดับ DNA ให้ด้วยได้มั้ยค่ะ ขอบคุณค่ะ
มาอ่านครับน่าสนใจมากๆครับอาจารย์
ตอนนี้พี่กำลังสนับสนุนให้ชาวบ้านเก็บสถิติปริมาณน้ำฝนกับอุณหภูมิในพื้นที่ทุกวัน และมาหาค่าความชื้นสัมพัทธ์ เพื่อเฝ้าสังเกตุปรากฏการณ์ต่างๆทางกายภาพของท้องถิ่นครับ
พี่จะลองเอาระบบตัวเลขนี้ไปสังเกตุสิ่งอื่นๆดูครับ
สวัสดีครับ
วันนี้อากาศดีมากๆครับ เลยซ่อมจักรยานลมล้อยางซึม แกะซ่อมแล้วหาไม่เจอรูรั่วหรือซึม เลยไม่รู้ว่าจะปะตรงไหน ก็เลยคิดว่าสงสัยไม่มีปัญหา ก็เลยปั่นไปเที่ยวกับน้องๆ ไปยังเมือง ลาเดนบวร์ก Ladenburg เมืองผลิตเบนซ์คันแรกของโลก ไม่อยากจะเชื่อว่าปั่นไปราวๆ 1 ใน 3 ของเส้นทาง ยางแบน สรุปว่ากว่าจะไปถึงเป้าหมาย สูบลมกัน 5 ครั้ง
และขากลับ สูบลมไปทั้งหมด 8 ครั้ง ห้าๆๆๆ นี่ขนาดไปปั่นจักรยานเล่น ยังเป็นลำดับ ฟิโบนักชีเลยครับ ห้าๆๆๆๆ
วันหน้าจะหาให้เจอว่า ซึมตรงไหนหนอล้อจักรยาน....
น้องๆ ผัดข้าวกับน้ำพริกไปทานที่เมืองลาเดนบวร์ก บรรยากาศดีๆ แดดดีๆ กินอาหารอร่อย สนุกจริงๆ ครับวันนี้ วันลดไขมันด้วยครับ
น่าจะชั่งน้ำหนักดู ไม่แน่อาจจะเป็นฟิโบนักชีด้วย ห้าๆๆๆๆ
เมื่อคืนฝันแต่งานวิจัยอย่างเดียวเลยครับ ห้าๆๆๆๆ คริๆๆๆ
ขอให้ทุกท่านสนุกกับชีวิต และความงามของชีวิต อยู่พอเพียง ไม่ต้องร่ำรวยแบบกราฟของฟิโบนักชีนะครับ แค่พอเพียงธรรมดา ค่อยเป็นค่อยไป ก็พอแล้วครับ ชีวิตนี้ ใช้ชีวิตให้เสถียรเหมือนกราฟที่ลู่เข้าของอัตรา่ส่วนทองก็พอแล้วครับ
ขอบคุณมากครับ
สวัสดีครับพี่แป๋ว paew
สบายดีไหมครับ น่าสนใจครัีบเรื่องที่พี่นำเสนอ แต่ผมเองไม่ค่อยมีความรู้ทางด้าน ดีเอ็นเอเ่ท่าไหร่ครับ สิ่งที่อยากให้พี่ลองดูก็คือว่า
ในหนึ่งรอบของเกลียว DNA หรือภาพที่พี่ส่งมานะครับ ว่าการบิดในหนึ่งรอบนั้นของสาย DNA หนึ่งรอบดูนะครับ ว่ามีกี่สาัยเชื่อมครับ ผมเชื่อว่าจะเป็นตัวเลขที่น่าสนใจเช่นกันครับ
การเชื่อมกับของโครงข่ายเหล่านั้นมีกฏเกณฑ์ต่างๆ ซึ่งต้องเข้าใจระบบของสิ่งนั้นๆ แล้วค่อยเอาคณิตศาสตร์ไปจับเพื่อจะอธิบายนะครับผม
ขอบคุณมากๆ นะครับ
สวัสดีครับคุณกวินทรากร
ขอบคุณมากครับ จะลองเอาคณิตศาสตร์ไปจับกับกลอนดูไหมครับ สร้างความสัมพันธ์การสัมผัสนอกใน ตามลำดับคำ นำไปสู่ความเข้าใจของการแต่งกลอนแบบสนุกๆ ครับ อิๆๆๆ จริงๆ ก็มีอยู่แล้วใช่ไหมครับ เผื่อจะสร้างกฏเกณฑ์ใหม่ๆครับ
ขอบคุณมากครับ
สวัสดีครับพี่บางทราย (คนเข็นครก ขึ้นภูเขา)
ยอดเยี่ยมมากๆ เลยครับ การมีข้อมูลเท่านั้นครับ ถึงจะมองอะไรออกครับ หากไม่มีข้อมูลในมือก็เท่ากับว่าตาบอดในเรื่องการวิจัยเลยครับ เป็นสิ่งที่ดีมากๆครับ ที่พี่เก็บข้อมูลครับ ปัจจัยทางอุตุนิยมวิทยาเกี่ยวข้องกับชีวิตทุกชีวิตแม้แต่การตลาดหรือดัชนีหุ้นครับ
ผมชอบที่คนสมัยก่อนเค้าใช้วิธีการสังเกตเอาและได้เป็นเงื่อนไขครับ แต่ทุกวันนี้ โลกเปลี่ยนแปลงครับ คำตอบเล่าจากอดีตบางอย่างต้องเก็บข้อมูลใหม่ครับ แต่บางอย่างก็ใช้ได้ตลอดครับ
ขอให้พี่สนุกในการวิัจัยนะครับผม ขอบคุณมากครับ
สวัสดีค่ะคุณเม้ง
รักธรรมชาตินะคะ คุณเม้ง แต่ตกคณิตศาสตร์ค่ะ เฮอๆ .. งง ค่ะ
... เห็น calla แล้ว คิดถึง calla หนังเกาหลี น่ารักม๊ากๆ
คุณเม้งคงไม่เคยดูล่ะสิ อิ อิ
... calla ที่นางเอกแอบมอบให้คนรักจาก 1,2, ... *
คุณเม้ง ลองใช้ สูตร fibonacci ดูสิคะ ว่า สุดท้าย ... รวมกันแล้ว ผลลัพธ์ เป็นเท่าใด ...
.. * ปล. based on revolution แบบทวนเข็มนาฬิกา นะคะ .. คิดออกบ่คะ
สวัสดีครับคุณเม้ง
สมัยเรียนหนังสือก็รู้จักแต่ Phyllotaxis พอทำงานสักพักก็รู้จักกับ Golden Ratio หาข้อมูลในเน็ต ก็เจอสัดส่วนนี้ในธรรมชาติจำนวนมาก บางเวปก็ได้รางวัลในการอธิบาย Fibonacci sequence แต่ก็เป็นภาษาอังกฤษทั้งหมด
มาวันนี้ ได้เจอ ธรรมชาติกับคณิตศาสตร์ ... จากฟิโบนักชีสู่โครงสร้างทางชีววิทยา ของคุณเม้งเข้า ทำให้เกิดความแตกฉานเพิ่มขึ้นขอบคุณสำหรับบันทึกดีๆแบบนี้ครับ
หึๆๆๆ....
- เรื่องคณิตศาสตร์ตามแบบของนักคณิตศาสตร์ พี่ครูวุฒิมึนตึ้บ
- แต่คณิตศาสตร์ของธรรมชาติ สวยน่าทึ่งมาก
- สวัสดีครับ
สวัสดีครัีบคุณปูpoo
สบายดีไหมครับ ปูมีแปดขา สองก้าม สองตา หนึ่งสะดือ อิๆๆๆ เลขในลำดับครับ....
ผมไม่รู้จักคอลล่าครับ....อยู่นี้บ่เคยดูบ่เคยฟังครัีบ
เลยบ่สามารถอธิบายได้ครับผม ต้องทราบข้อมูลก่อนนะครัีบ
สบายดีนะครัีบ...ฝั่งลาวเป็นไงบ้างครัีบ
ขอบคุณมากครัีบ
สวัสดีครับลุงพูน
สบายดีไหมครับ คิดถึงๆ ครับผม สวนเกษตรธรรมชาติเป็นอย่างไรบ้างครับ ไม่ค่อยได้ติดตามเลยครับ
เรื่องอัตราส่วนทอง นี่เป็นตัวเลขที่มีความมหัศจรรย์มากนะครับ
- ตัวของมันเอง หารด้วย หนึ่ง จะมีค่าเท่ากับ หนึ่งหารด้วยตัวของมันที่ลบออกจากหนึ่ง
Phi / 1 = 1 / (Phi -1 )
- ค่านี้ได้จาก สี่เหลี่ยมฟิโบนักชีนะครับ ลองศึกษาเพิ่มเติมได้จากหลายๆ ที่นะครับ
- ความรู้ที่เราได้มาและมีอยู่ทุกวันนี้ ล้วนได้มาจากธรรมชาติทั้งสิ้นครัีบ ไม่มีธรรมชาติไม่มีความรู้ แต่เราก็ยังทำลายธรรมชาติอยู่ตลอดนะครัีบ
รักษาสุขภาพครับ
สวัสดีครับคุณครูครูวุฒิ
ขอบคุณมากครัีบ เลขก็ได้จากธรรมชาติครับ ส่วนตัวเลขเป็นเพียงสัญลักษณ์ครับ ความหมายสำคัญกว่าสัญลักษณ์ครับ ความหมายจากธรรมชาติ แปลงเป็นชุดของสัญลักษณ์ แต่ท้ายสุดก็ต้องแปลความเหมือนกันครับ
สนุกในการทำงานพอเพียงให้เพียงพอนะครับ
สวัสดีค่ะ ชื่อปริมนะคะเรียนคณิตศาสตร์ปีสามแล้ว
กำลังจะทำโปรเจคท์สนใจเรื่องนี้มากๆค่ะ
ช่วยให้คำแนะนำได้มั้ยคะ
comepai เด็กวิทย์ห้อง King
สวัสดีค่ะ ขอบคุณมากนะค่ะสำหรับข้อมูลดีๆแบบนี้และอย่างน้อยมันก็ทำให้หนูมีงานส่งอาจารย์ค่ะ แต่สิ่งที่น่าแปลกใจก็คือทำไมสิ่งดีๆมีสาระแบบนี้เด็กมัธยมแบบหนูถึงไม่ค่อยสนใจกันนะ หนูจะพยายามเข้ามาบ่อยๆนะค่ะเพราะคุณเริ่มทำให้หนูชอบคณิตศาสตร์แล้วละค่ะ
ป.ล. การที่คุณถามว่า สบายดีมั้ยครับ มันเป็น ฟิโบนักชี ด้วยหรือเปล่าค่ะ ดูเหมือนว่ามันจะเพิ่มขึ้นเรื่อยๆตามจำนวนคนนะค่ะ 555+++
น่าสนใจมากๆค่ะ เปรียบเทียบกับดอกไม้ด้วย เลยดูน่าสนุกมากๆ
จากสาวร้านดอกไม้ค่ะ
เด็กหล่อรวยเก่ง
คือผมอยากได้ภาพที่เกี่ยวกับทฤษฏีของเขาอ่ะครับ แบบว่าไม่เคลื่อนไหวอ่ะครับ มีมั้ยครับ แบบหยุดให้ที
ขอบคุณครับ
ต่วนฮาฟีฟะห์ บินสุหลง
เก่งมากเลยอาจรย์เรา
ทำไมอาจารย์ถึงเก่งขนาดนี้
เรียนกับอาจารย์แล้วรู้สึกว่าได้เห็นถึงความงามของคณิตศาสตร์มากขึ้น(โดยเฉพาะในการทำโครงงาน)
อาจารย์คะ นู๋ชอบหัวข้อนี้มากเลยคะ นู๋จะเอาหัวข้อนี้เป็น หัวข้อสัมมานา น่าสนใจ อาจารย์ช่วยแนะแนวทางหน่อยนะค่ะ
สวัสดีค่ะพี่เม้ง^ ขอบคุนสำหรับคำแนะนำดีๆสำหรับเลขฟีบอนาชีนะคะ เพราะตอนนี้หนูอยู่ม.5กำลังทำโครงงานเรื่องนี้ิอยู่เลยค่ะ ตอนแรกคิดอะไรไม่ออกเลยค่ะว่าจะเอาอะไรมาศึกษาเลขฟีบอนาชีดี แต่พอได้อ่านที่พี่โพสแล้วทำให้หนูมีแนวทางในการทำโครงงานขึ้นมากเลยค่ะ ขอบคุนมากๆเลยนะคะ
มีสูตรที่ทำให้หาได้ง่ายไหมค่ะ
อยากทราบว่า ต้องกี่เลขขึ้นไปถึงไปถึงจะเรียกว่า เป็นลำดับฟีโบนัชชีแล้ว อย่างเช่น 2 3 5 เรียงกันก็เป็นได้เลยรึป่าว ค้ะ