Simpson's Paradox, Interaction และ Confounding
บทที่ 10, A collection of power-point presentationsdeveloped from the ActivEpi CD text จาก www.openepi.com
Table แปลว่าตาราง, แปลว่าโต๊ะ
การรวม 2 ตาราง โดยรวมหมวก จากโต๊ะ 2 ตัวไป รวมใว้บนโต๊ะตัวเดียว
ใต๊ะเป็นตัวแปรที่ 3 ที่เพิ่มขึ้นมา คือ Table1, Table2
เพิ่มจากตัวแปรต้น (Green, Blue) และตัวแปรตาม (Fit, Not Fit)
การรวม 2x2 table 2 ตาราง (Stratum1, Stratum2) เข้าด้วยกัน
ให้เป็นตารางเดียว (Crude)
และเรื่องของการ รวม 2 โต๊ะ (Tables) เข้าด้วยกันเป็นโต๊ะเดียว (Combined)
ของห้างขายหมวก Simpson's
การรวมโต๊ะ 2 โต๊ะ เข้าด้วยกัน (Combined) แต่ได้ผลขัดแย้งกัน (Paradox)
กับการผู้สังเกต ของผู้ขายแต่ละโต๊ะ (Stratified strata)
ตัวแปรต้น คือ สีของหมวก เขียวและน้ำเงิน (Green, Blue)
ตัวแปรตาม คือ ลูกค้าสวมได้พอดีหรือไม่ (Fit, Not Fit)
ตัวแปร 3 คือ โต๊ะที่ใช้วางหมวก (Table 1, Table 2)
หมวกโต๊ะละ 16 ใบ
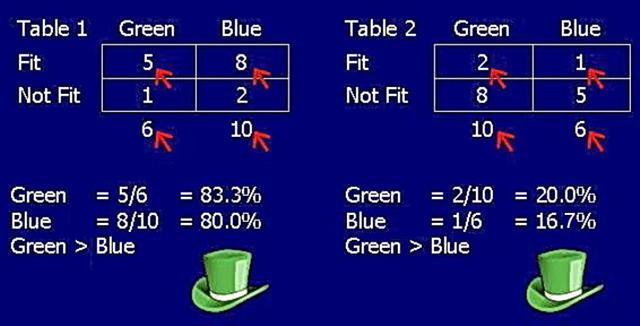
Table1 Green 83.3% (n=6) > Blue 80.0% (n=10)
Table2 Green 20.0% (n=10) > Blue 16.6% (n=6)
(Green > Blue)
ผู้ขายที่โต๊ะ 1 และโต๊ะ 2 บอกว่าหมวกสีเขียวลูกค้าใส่ใด้พอดีได้มากกว่า
แต่วันรุ่งขึ้นเมือผู้จัดการให้รวม 2 โต๊ะเป็นโต๊ะเดียว
โต๊ะเดียวกันมีหมวกสีเขียว 16 ใบและสีน้ำเงิน 16 ใบ
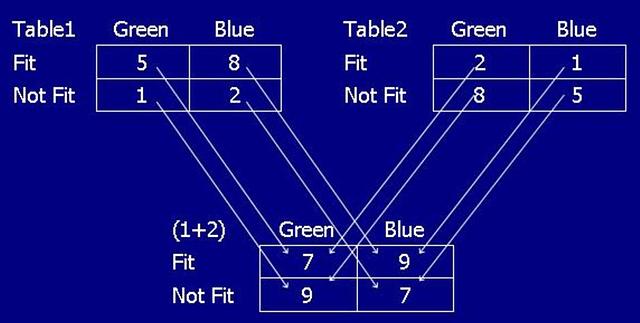
เมื่อรวมสองโต๊ะเป็นโต๊ะเดียว
พบว่าหมวกสีน้ำเงิน (Blue) ลูกค้าใส่ได้พอดีมากกว่า (กลับทิศทาง*)
(1+2) Green 44.75% (n=16) < Blue 56.25% (n=16)
----------------------------------------------------------------------------------------------
Table1 Green=5/6 Blue=8/10
Table2 Green=2/10 Blue=1/6
(1+2) Green=7/16 Blue=9/16
Table1 Green 83.3% (n=6) > Blue 80.0% (n=10)
Table2 Green 20.0% (n=10) > Blue 16.6% (n=6)
(1+2) Green 44.3% (n=16) < Blue 56.2% (n=16) กลับทิศทาง*
"ควรจะเชื่อผู้ขายแต่ละโต๊ะที่บอกว่าหมวกสีเขียวลูกค้าใส่ได้พอดีมากกว่า ?
หรือว่า จะดูที่ผลรวมว่าหมวกสีน้ำเงินลูกค้าใส่ได้พอดีมากกว่า ?"
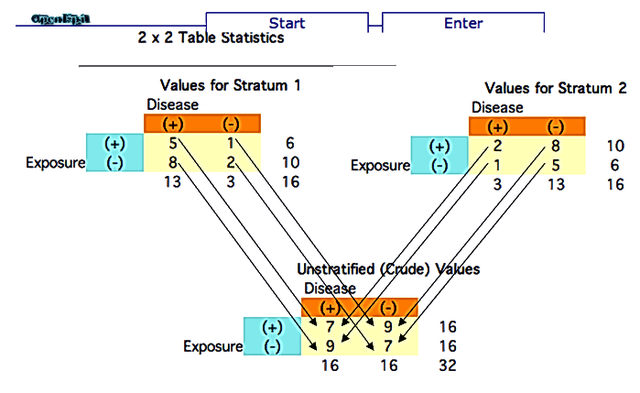
การจัดวาง Row และ Column ของ table1, 2 และ (1+2) เช่น เดียวกับ STATA
ที่วาง Exposure หรือ Predictor ไว้ด้านบน (คำนวณ Risk แบบ Column%)
คราวนี้จะใช้ OpenEpi คำนวณค่า RR
ของ table1, table2, Crude RR, Adjusted RR
รวมทั้ง 95%CI ของ RR และ Breslow-Day test for Interaction
เนื่องจาก Openepi และ Epiinfo
กำหนดให้ Outcome หรือ Event หรือ Respond ไว้ด้านบน
Exposure หรือ Predictor ไว้ด้านซ้าย (คำนวณ Risk แบบ Row%)
จึงต้องปรับทิศทาง table ใหม่ โดยให้ Exposure(+,-) คือ (Green, blue)
และ Disease(+,-) คือ (Fit, Not Fit)
แล้วลงข้อมูลใน 2x2 table ของ Openepi www.openepi.com
หมุนทิศของ Table
เพื่อที่ openepi จะได้คำนวณ Risk แบบแถวแนวนอน (คำนวณ Risk แบบ Row%)
คำนวณ RR ของ table 1 จาก Green 5/6 และ Blue 8/10
คำนวณ RR ของ table 2 จาก Green 2/10 และ Blue 1/6
คำนวณ Crude RR จาก Green 7/16 และ Blue 9/16
Fit = Dis (+), Not Fit = Dis (-)
เขียว Green = Exp (+) [ ][ ]
น้ำเงิน Blue = Exp (-) [ ][ ]
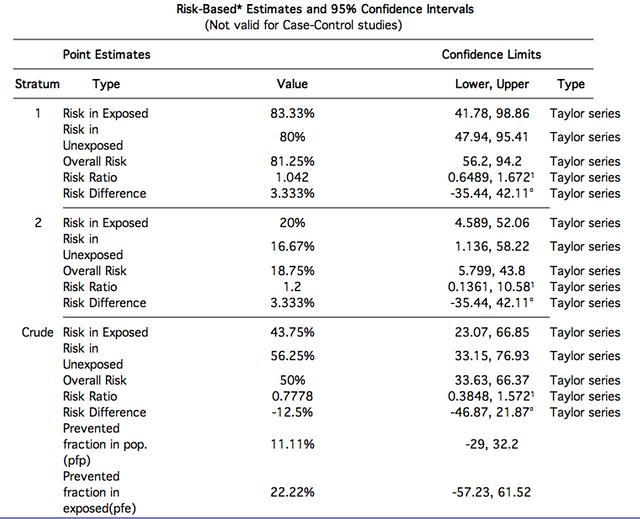

Risk Ratio (RR)
Breslow-Day test for interaction of Risk Ratio over strata p=0.9009
p > 0.05 คือไม่มี Interaction ใช้วิธีรวมโต๊ะได้ และใช้ค่า Adjusted RR ได้
แต่ว่า 95% CI ของ Adjusted RR มีค่า 1 รวมอยู่ด้วย (95%CI of RR included 1)
Crude RR= 0.77 (95%CI 0.38 to 1.57)
M-H Adjusted RR= 1.069 (95%CI 0.61 to 1.86)
95% RR มีค่า 1 รวมอยู่ด้วยคือ RR จึงมีโอกาสเป็น 1 ได้
Risk Difference (RD)
นำค่า Risk Ratio ระหว่าง strata มาลบกัน (RR1 - RR2)
Breslow-Day Test for interaction of Risk Difference over strata p>=0.9999
(ถ้า p < 0.05 สนับสนุนมี Interaction นำเสนอโดยใช้ค่า Risk Difference แยกแต่ละโต๊ะ)
Stratum1 RR > 1 เป็นปัจจัยเสี่ยง
Stratum2 RR > 1 เป็นปัจจัยเสี่ยง
Crude RR <1 กลับทิศทาง เป็นปัจจัยป้องกัน
M-H Adjusted RR = 1.069 (95%CI 0.61 to 1.86)
แต่ว่า 95%CI มี 1 รวมอยู่ด้วย
Adjusted RR ไม่เท่ากับ Crude RR คือมี Confounding
"ควรจะเชื่อผู้ขายแต่ละโต๊ะที่บอกว่าหมวกสีเขียวลูกค้าใส่ได้พอดีมากกว่า ?
หรือว่าจะดูที่ผลรวมว่าหมวกสีน้ำเงินลูกค้าใส่ได้พอดีมากกว่า ?"
Var1 (Green, Blue)
Var2 (Fit, Not Fit)
Var3 (Table1, Table2)
ไม่มี Interaction ของ Var3
Table1 (RR=1.04 95%CI 0.64 to 1.67)
Table2 (RR=1.2 95%CI 0.13 to 10.58) ต่างกันไม่มากนัก
p > 0.05 ไม่มี Interaction
มี Confouning ของ Var3
Crude (RR=0.77 95%CI 0.38 to 1.57) ต่างกันกับ
Adjusted (RR=1.06 95% CI 0.61 to 1.86)
คำถาม
ควรเชื่อถือ RR ของ Table1 หรือ RR Table2 ?
หรือควรเชื่อถือ RR ของ Crude ?
ตอบ
ไม่มี Interaction
(จาก Breslow-Day p>0.05 สามารถใช้ Adjusted RR ได้)
มี Confounding
Crude (RR=0.77 95%CI 0.38 to 1.57)
Adjusted (RR=1.06 95% CI 0.61 to 1.86)
เลือกใช้ Adjusted RR
ซึ่งหมายความว่า Green Fit > Blue = 1.06 เท่า
แต่ Adjusted RR 95% CI มี 1 รวมอยู่ด้วย
จึงทำให้ Adjusted RR มีน้ำหนักไม่มากพอที่จะยืนยันคำตอบได้
RR (ของ Table1, Table2, Crude, M-H Adjusted)
95% CI มี 1 รวมอยู่ด้วยทุกอัน การแปลผล RR จึงต้องดูที่ 95% CI ด้วย
ตัวแปรตัวที่ 3 เป็นทั้ง effect modification และ confoundingได้
ไม่ใช่ว่าจะเป็น effect modification
หรือ confounding ได้เพียงอย่างใดอย่างหนึ่ง คือ not mutually exclusive
(คือวงกลมขอบเขตของ effect modification
อาจจะซ้อนกันบางส่วนกับวงกลม ของ confounding)
การที่พบว่ามี effect modification เป็นสิ่งสำคัญ
(ซึ่งจะเป็น Confounding ด้วยหรือไม่ มีสำคัญน้อยกว่า)
หมายถึงการนำเสนอข้อมูลควรจะแยกชนิด ตาม Stratum
ไม่ใช่เสนอแบบรวมทั้ง 2 ชนิดแบบ Summary
1. effect modifiers และ confounders ส่งผลไปที่ Outcome
confounders ทำให้เกิดโรคโดยที่เป็นอิสระจากสิ่งที่คาดว่าก่อโรค (Exposure)
แต่ effect modifiers ไปเปลี่ยนแปลงการทำงานของสิ่งที่คาดว่าก่อโรคต่อการเกิดโรค
2. ถ้าตัวแปรนั้น
จะเป็น confounders ตัวแปรที่ 3 นั้นจะต้องเกี่ยวข้องเกี่ยวเนื่องกันกับสิ่งที่คาดว่าก่อโรค
(มี Association ไม่เป็นอิสระจากกัน กับ Exposure)
ซึ่งสำหรับการที่จะเป็น effect modifier ไม่จำเป็นจะต้องเกี่ยวข้องเกี่ยวเนื่องกันกับสิ่งที่คาดว่าก่อโรค
3. ถ้ามี effect modifiers การนำเสนอข้อมูลควรจะแยกชนิด ตาม Stratum
ไม่ใช่เสนอแบบรวมทั้ง 2 ชนิดแบบ Summary
ซึ่งต่างจากเรื่อง Confounding ซึ่งเป้าหมายคือต้องการกำจัดผลจาก Confounding ออกไป
Openepi :ในส่วน
Kevin's Webpage
http://www.sph.emory.edu/~cdckms/
http://www.sph.emory.edu/~cdckms/CONF2f.zip
Extract ได้ เป็น CONF2f.doc 22-Jun-2005
page 13/33 อธิบาย effect modification และ confounding
Simpson's Paradox, Odds Based
http://www.gotoknow.org/blogs/posts/499018
ความเห็น (0)
ไม่มีความเห็น