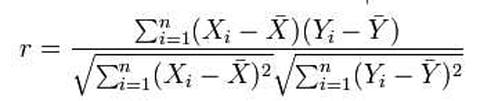สัมประสิทธิ์สหสัมพันธ์ เกิดจากแนวคิดเรื่องเวกเตอร์

สิ่งที่ล้อตามกัน ก็เหมือนเวกเตอร์สองเส้นที่ชี้ไปทางเดียวกัน

สิ่งที่แย้งกัน ตรงข้ามกัน ก็เหมือนเวกเตอร์ที่ชี้ตรงข้าม

สิ่งที่ไม่ขึ้นแก่กัน ก็จะเหลือทางเลือกเดียว ไม่ตาม ไม่แย้ง ก็คือ ต้องตั้งฉาก

เราจะรู้ได้อย่างไรว่าเวกเตอร์ชี้ไปทางไหน

เขาใช้ผลคูณ dot product ของสองเวกเตอร์ มาช่วยอนุมานมุมระหว่างสองเวกเตอร์ ก็จะทราบว่าเวกเตอร์ชี้ทำมุมกันอย่างไร

ถ้า A และ B เป็นเวกเตอร์

A⋅B = ∑ a(i) * b(i)

เมื่อ i คือลำดับที่ของข้อมูล โดยเวกเตอร์ A มีสมาชิกย่อย ๆ เป็น a(1), a(2). ... ตามลำดับ B ก็จะมี b(1), b(2),... ทำนองเดียวกัน

เห็นสมการยุ่ง ๆ อาจคิดในใจว่า โห ยากจัง

อย่าตกใจ เด็กประถมก็ใช้สูตรนี้เป็นตามสัญชาติญาณแล้ว

เวลาเด็กไปซื้อขนม ซื้อปีโป้สองชิ้น ชิ้นละ X บาท ซื้อกูลิโกะสามกล่อง กล่องละ Y บาท ซื้ออมยิ้ม 4 อัน อันละ Z บาท

เด็กจ่ายเงินรวม = 2X + 3Y + 4Z

ทำไมเอา 2 คูณ X ไม่ไปคูณ Y หรือ Z ?

เพราะมันไม่เกี่ยวไง

ซื้ออะไร ก็ต้องเอาราคาต่อชิ้นสิ่งนั้น คูณจำนวนหน่วยสิ่งนั้น ถูกไหม

ถ้า A คือเวกเตอร์ของราคาสินค้าต่อหน่วย

และ B คือเวกเตอร์ของจำนวนหน่วยของสินค้าแต่ละชนิด

จ่ายเงินรวม ก็ต้องเป็นผลบวกของ จำนวนหน่วยสินค้า คูณ ราคาสินค้านั้น ๆ ต่อหน่วย

เงินที่จ่ายนี้ ก็คือ A⋅B นั่นเอง

เราเอาเวกเตอร์คูณกัน เกิดเป็นตัวเลขเดี่ยว ๆ ที่ไม่มีทิศทาง กลายเป็นปริมาณสเกลาร์

เกิดอะไรขึ้น ถ้า A เป็นเวกเตอร์มีขนาดยักษ์ และ B เป็นเวกเตอร์ขนาดเล็ก

A⋅A ก็จะกลายเป็นตัวเลขใหญ่มหึมา และ B⋅ฺB ก็จะกลายเป็นตัวเลขเล็กกระจ้อยร่อย

A⋅B เราคาดว่า มันน่าจะมีขนาดกลาง ๆ เป็นค่าเฉลี่ยระหว่าง A⋅A กับ B⋅ฺB

พวกนี้ เป็นตัวเลขหมด ไม่ว่า A⋅B, A⋅A หรือ B⋅ฺB

ค่าเฉลี่ยระหว่าง A⋅A กับ B⋅ฺB น่าจะเป็นค่าเฉลี่ยเรขาคณิต เพราะไม่งั้น คู่ไหนคูณกันแล้วเลขมาก ก็จะมีผลท่วมท้นกลบผลของอีกตัวไปหมด

ดังนั้น ค่าที่คาดหมายของ A⋅B ควรเป็น = √[(A⋅A)*(B⋅ฺB)]

(ค่าเฉลี่ยเรขาคณิต คือรากที่สองของผลคูณ)

ถ้า A ไปทางเดียวกับ B จริง A⋅B ต้องเท่ากับ √[(A⋅A)*(B⋅ฺB)]

ดังนั้น อัตราส่วน A⋅B / √[(A⋅A)*(B⋅ฺB)] จะบอกว่า มีความสอดคล้องกันระหว่างค่าที่คำนวณได้จริง A⋅B กับค่าที่ควรเป็น √[(A⋅A)*(B⋅ฺB)] แค่ไหน

อัตราส่วนนี้ ก็คือค่า r หรือ correlation coefficient นั่นเอง กล่าวคือ พอเป็นเวกเตอร์ เขามีคณิตศาสตร์ที่เกี่ยวกับเวกเตอร์ ก็แค่แทนค่าเข้าไปตามขั้นตอนที่ควรเป็นของคณิตศาสตร์แขนงนั้น

ซึ่งท้ายสุด ก็จะได้สมการนี้

ดังที่เคยกล่าวมาแล้วในตอนก่อนหน้านั่นเอง

ใช้สมการแทนรูปก็แล้วกัน เดี๋ยวจะว่า เรียนสถิติด้วยภาพ...ซะเมื่อไหร่