ว่าด้วยเรื่องสถิติ 5 : หลุมพรางของการเปรียบเทียบทางสถิติ
การบอกว่าเพศชายสนใจทำ R2R มากกว่าเพศหญิงนั้นเป็นการสรุปจากสายตา โดยเอาค่าร้อยละของเพศชายที่สนใจทำ R2R มาเปรียบเทียบกับร้อยละของเพศหญิงที่สนใจทำ R2R แล้ว เพศชายมากกว่า ก็เลยสรุปว่าเพศชายสนใจทำ R2R มากกว่า ตรงนี้ถือว่าเราได้ตกหลุมพรางของตัวเลขเข้าแล้ว แม้ว่าภาพที่เราเห็นจะเป็นเช่นนั้นก็ตาม
ในทางสถิติ การเปรียบเทียบกลุ่มตัวอย่าง 2 กลุ่ม ในเรื่องใดเรื่องหนึ่งนั้น จะต้องมีการตั้งสมมติฐานว่ากลุ่มตัวอย่างทั้งสองกลุ่มมีค่าเฉลี่ยไม่ต่างกัน แล้วหาทางพิสูจน์ว่าค่าเฉลี่ยของกลุ่มตัวอย่างทั้งสองกลุ่มไม่แตกต่างกันจริง ถ้าพิสูจน์ได้ว่าค่า p value มีค่ามากกว่า 0.05 แสดงว่าเรายอมรับสมมติฐานว่าค่าเฉลี่ยของกลุ่มตัวอย่างทั้งสองกลุ่มนั้นไม่แตกต่างกัน ก็เข้าใจได้ว่ามันเหมือนกันก็แล้วกัน ส่วนถ้าค่า p value น้อยกว่า 0.05 แสดงว่าเราไม่สามารถปฏิเสธได้ว่ามันเหมือนกัน ภาษาเข้าใจยากอีกแล้ว เอาเป็นว่ากลุ่มตัวอย่างทั้งสองกลุ่มมีค่าเฉลี่ยแตกต่างกัน เรื่องนี้เอาเป็นว่าผมค่อยอธิบายให้ฟังอย่างละเอียดทีหลังก็แล้วกัน
ทีนี้ลักษณะข้อมูลของเราเป็นตัวอักษร ภาษาสถิติเขาเรียกว่านามบัญญัติ (nominal scale) ฟังแล้วก็เข้าใจยากอีก เอาเป็นว่าข้อมูลที่เราเก็บเป็นตัวอักษร อย่างเช่น เพศชาย เก็บเป็นตัว M แล้ว เพศหญิง เก็บเป็นตัว F บางคนบอกว่าฉันเก็บเป็นตัวเลข ให้ 1 เท่ากับผู้ชาย แล้ว 2 เท่ากับผู้หญิง ฉันไม่ได้เก็บเป็นตัวอักษร เอ้า เป็นตัวอักษรหรือเป็นตัวเลขก็ได้ แต่ถ้าเป็นตัวเลขก็ใช้เปรียบเทียบค่ากันไม่ได้ ในที่นี้ หมายถึง เก็บเป็น 1 กับ 2 ซึ่งเลข 2 ในที่นี้ก็ไม่ได้หมายความว่ามีค่ามากกว่า 1 อย่างนี้พอจะเข้าใจไหม ข้อมูลลักษณะนี้ เวลาเปรียบเทียบกัน เขาวิเคราะห์ด้วยสถิติแบบนอนพาราเมตริกครับ โดยใช้สถิติที่เรียกว่า ไคว์สแคว์ (chi square) อย่าลืมครับว่าเราสัญญากันแล้วว่าไม่ต้องไปดูวิธีคำนวณ แค่นึกว่าเราจะใช้ไคว์สแคว์ ก็แค่กด Crosstab แล้วติ๊กเลือกสถิติ ไคว์สแคว์ แล้วมันก็โผล่ออกมา เราไปดูกัน
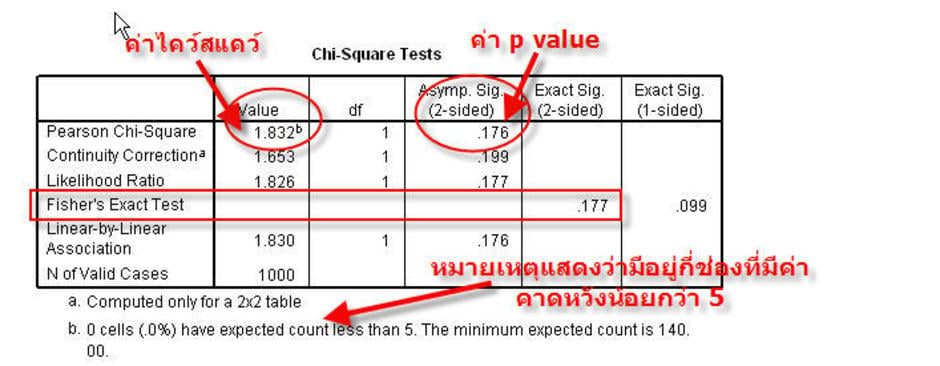
ในที่นี้ จะมีค่าตัวอื่นๆออกมาด้วย แต่ตัวแรกที่เราสนใจก็คือค่า ปัวซองไคว์สแคว์ ได้ค่า 1.832 แต่ก็ยังแปรผลยากอีก เพราะต้องเอาค่าที่ระดับนัยสำคัญมาเทียบ เราข้ามไปดูค่าที่เราใช้กันดีกว่า นั่นคือค่า asym sig 2 side หรือค่า p value ที่เรารู้จักกันดี อย่าลืมนะครับว่า ค่านี้จะใช้เทียบกับค่า 0.05 ถ้าค่า p value มากกว่า 0.05 แสดงว่าค่าเฉลี่ยของกลุ่มตัวอย่างที่สองเพศไม่ต่างกัน แต่ถ้าค่า p value น้อยกว่า 0.05 แสดงว่าค่าเฉลี่ยของกลุ่มตัวอย่างทั้งสองเพศแตกต่างกัน แล้วตัวเลขที่ออกประจำงวดนี้ ได้แก่ ….0.176 ไชโย ! มีค่ามากกว่า 0.05 ค่าเฉลี่ยของทั้งเพศชายและเพศหญิงไม่แตกต่างกันครับ บอกแล้วไงว่าที่เราเห็นตั้งแต่ต้นมันเป็นเพียงภาพลวงตา ของจริงต้องใช้สถิติช่วยครับถึงจะเห็นว่าต่างจริงหรือเปล่า
เมื่อเริ่มเข้าใจหลุมพรางหลุมแรกแล้ว ก็อย่าตกหลุมที่สองอีก ไม่ใช่ว่าไคว์สแคว์จะใช้ได้ในทุกเรื่องครับ มันมีข้อกำหนดในการใช้อยู่ เราไปดูกัน
- ข้อแรก บอกเอาไว้ว่า ใช้ในการวิเคราะห์ข้อมูลที่เป็น นามบัญญัติ ก็อย่างที่ได้อธิบายไว้แล้วข้างต้นครับ
- ข้อสอง กลุ่มตัวอย่างทั้งสองกลุ่มที่นำมาเปรียบเทียบกัน ต้องไม่ขึ้นแก่กัน เป็นอิสระต่อกัน เอ ! แล้วจะอธิบายยังไงดีนะ ในที่นี้กลุ่มตัวอย่างที่เป็นเพศชาย กับที่เป็นเพศหญิง เป็นคนละกลุ่ม ไม่ขึ้นแก่กัน ฟังดูอาจจะยังไม่เข้าใจอีก เราลองไปดูกลุ่มตัวอย่างแบบที่ไม่เป็นอิสระหรือบางครั้งเขาเรียกว่ากลุ่มตัวอย่างมีความสัมพันธ์กันดีกว่า อย่างเช่น การเปรียบเทียบนักเรียนห้องเดียวกัน ทำข้อสอบ Pretest ก่อนเรียน แล้วก็ Posttest หลังเรียน แล้วเอาคะแนนมาเทียบกัน อย่างนี้ถือว่าเป็นกลุ่มตัวอย่างที่มีความสัมพันธ์กัน ไม่เป็นอิสระกัน เพราะนักเรียนคนที่ 1 ที่ทำ Pretest กับ Posttest เป็นคนเดียวกัน ก็เลยไม่เป็นอิสระต่อกัน พอจะเห็นภาพลางๆบ้างไหม
- ข้อสาม ค่าไคว์สแคว์ใช้ได้ในกรณีที่ไม่มีข้อมูลในช่องใดช่องหนึ่งมีค่าคาดหวังน้อยกว่า 5 ลงมาไอ้ค่าคาดหวังนี้เป็นค่าคำนวณครับ เราสัญญากันแล้วว่าจะไม่คำนวณ ปกติตรงท้ายตารางของไคว์สแคว์ (ดูหมายเหตุ b ในตาราง) จะบอกไว้ว่าในตารางมีอยู่กี่ช่องที่มีค่าคาดหวังน้อยกว่า 5 ซึ่งถ้าเจอตรงนี้เมื่อไหร่ ก็ให้รู้ไว้เลยครับว่าใช้ค่า ไคว์สแคว์ตรงๆ ไม่ได้ ต้องหนีไปใช้ค่า Adjust chi square หรือ Yates’ chi square ซึ่งรู้สึกว่า บน SPSS จะไม่มีค่าตัวนี้ แต่คำนวนบน web ได้ครับ ลองไปใช้ที่นี่ครับ http://www.quantpsy.org/chisq/chisq.htm จะมีทั้งค่า ไคว์สแคว์ และ Yates’ chi square สามารถคำนวณได้เลยครับ ในกรณีนี้บางคนบอกว่าถ้าตัวอย่างตรวจไม่มากสามารถใช้ค่า Fisher’s Exact test ได้ครับ ถ้าใช้ค่านี้ ก็อยู่ที่บรรทัดที่ 4 ในตารางเดียวกันครับ โดยให้ดูที่ Exact Sig 2 side เป็นค่า p value แล้วเปรียบเทียบเหมือนกันครับ (ที่เรากำลังคุยกันอยู่นี้ผมยกตัวอย่างสำหรับข้อมูลที่อยู่ในตาราง 2 x 2 นะครับ หากตารางใหญ่กว่านี้ ค่อยว่ากันตอนหน้าครับ
ความเห็น (14)
อรุณสวัสดิ์ค่ะ คุณไมโต
- อ่านแล้วสนุกและได้รับความรู้ด้วย ครูผู้สอนพยายามใช้คำศัพท์ง่ายๆในการพูดแล้วเข้าใจ
- ครูอ้อยถามครูไมโตว่า "วันหนึ่งครูอ้อยไปฟังรุ่นพี่สัมมนาปฏิบัติการครั้งที่ 2 และพี่เขาพูดถึง chi square แต่เธออ่านว่า ชิ สแควร์ "
- ครูอ้อยหันมามองเพื่อนข้างๆ และใช้ดวงตายิ้มกัน พี่เธอพูดผิดใช่ไหมคะ ที่ใช้ดวงตายิ้มเพราะเกรงว่าจะเสียมารยาทค่ะ
- ครูอ้อยเข้าใจ หลุมพราง เข้าใจค่า p vulue และเข้าใจ เป็นอิสระต่อกันค่ะ เข้าใจเยอะไหมคะ
- ดีนะที่อ่านตอนเช้า เขาใจดีค่ะ ครูไมโต
- จะรีบไปโรงเรียนค่ะ ไปทำงานที่โรงเรียน ลูกเล่าให้ฟังว่า วันนี้แฟลตจะปิดไฟฟ้าทั้งวัน ซ่อมอะไรก็ไม่ทราบค่ะ
- บ๊ายบาย
- ดีใจจังเลย ที่ครูอ้อยบอกว่าเข้าใจ
- ผมล่ะกลุ้มใจอยู่นานว่าจะเขียนอย่างไร ให้อ่านแล้วเข้าใจ
- สงสัยคำนี้คงอ่านได้หลายแบบมังครับ ครูอ้อย อย่างเช่น ไคว์ สแคว์; ชิ สแคว์ แล้วก็ยังมี ไช สแคว์ อีกหน่อยก็คงจะถึงสยาม สแคว์ เอเดี่ยวนี้ยังจะมีอยู่อีกหรือเปล่าหนอ ไม่ได้เข้ากรุงเทพนานแล้ว
ค่า Yates’ chi square และ Fisher’s Exact test เราจะตัดสินใจใช้ต่างกันนะครับ โดยค่า Yates’ chi square จะใช้เมื่อเราดำเนินการยุบเซลล์แล้ว สุดท้ายเหลือเป็นตาราง 2X2 (เมื่อยุบรวมได้ตามข้อตกลงของการยุบรวมเซลล์) ค่าที่คำนวณออกมาและไม่มีเซลล์ที่มีค่าคาดหวังน้อยกว่า 5 แล้ว หากว่ายังมีอีกคราวนี้แหละครับเราจะไปใช้ค่า Fisher’s Exact test ส่วนนี้ผมเคยทดสอบโดยใช้ตัวเลยสมมติ ค่า Yates’ chi square และ Fisher’s Exact test แตกต่างกันครับ หากไม่คำนึงส่วนนี้ (หมายเหตุ: ตารางที่ใช้คำนวณค่า chi square จะมีข้อตกลงเบื้องต้นว่าต้องมีเซลล์ที่มีค่าคาดหวังที่น้อยกว่า 5 ได้ไม่เกิน 20% ของเซลล์ทั้งหมด หากเป็นตาราง 2X2 แล้ว มี 1 เซลล์ ก็เป็น 25% เข้าไปแล้ว)
สมัยที่กำลังเรียนต่อและได้เรียน Advance Statistic ผมลองไปสุ่มเลือกหยิบ Thesis ที่ใช้ chi square ในห้องสมุดมหาวิทยาลัยแห่งหนึ่งมาดู 10 เล่มที่ใช้ chi square พบว่ามีการละเมิดข้อตกลงเบื้องต้นในหลาย ๆ ส่วนมากน้อยในแต่ละเล่ม จำนวน 8 เล่ม ที่ไม่พบว่ามีการละเมิดและสังเกตได้ถึงความพยายามในการจัดการกับข้อมูลเป็นอย่างดีมีเพียง 2 เล่ม ที่พบว่าละเมิดมากที่สุดเลยก็คือวิเคราะห์และแปลผลไปทั้ง ๆ ที่ยังมีเซลล์ใดเซลล์หนึ่งมีค่าสังเกตเท่ากับศูนย์ ผมมองว่าการการที่เราจะเสพงานวิจัยเพื่อนำมาใช้และเชื่อตาม ๆ กันไปตามที่เขาสรุปไว้ คนเสพคงต้องระมัดระวังและตรวจสอบให้มากด้วยครับ
ขอบคุณนะครับที่นำมาถ่ายทอดไว้และผมก็ได้ทบทวนขึ้นมาอีก หากไม่มีบันทึกนี้ ผมคงไม่ได้นึกที่จะทบทวนครับ และที่ผมเขียนไว้ข้างต้นก็อาจจะมีที่ผมยังรู้ไม่ชัดแจ้งนัก ยินดีที่จะแลกเปลี่ยนกันต่อนะครับ
สวัสดีค่ะ คุณไมโตและคุณชายขอบ
- ครูอ้อยอ่านบันทึกของคุณไมโตเข้าใจแล้ว มาอ่านของคุณชายขอบยิ่งเข้าใหญ่เลย ดีจัง ครูอ้อยไม่ต้องเข้าห้องเรียนก็เข้าในเรื่อง chi square
ขอบคุณท่านทั้งสองค่ะ
- ขอบคุณครับคุณชายขอบ ที่ช่วยเติมเต็มให้สมบูรณ์ยิ่งขึ้น
- ตอนแรกคิดว่าจะเขียนแบบไม่ลงลึก เพราะไม่อย่างนั้นจะต้องอธิบายข้อปลีกย่อยค่อนข้างเยอะ ตั้งใจว่าจะเขียนแนะนำไปการใช้สถิติไปทีละตัว ให้เห็นภาพว่าเขาเอาไปใช้กันอย่างไร
- แต่เรื่องไคว์สแคว์นี้อาจต้องต่อภาค 2 แล้วล่ะครับ
- ต้องขอออกตัวนิดนึงก่อนว่าผมไม่ใช่ผู้เชี่ยวชาญด้านสถิติ ที่จะรู้ถึงที่มาของค่าสถิติแต่ละตัว เพียงแต่ผมพอจะมีโอกาสได้ใช้สถิติเหล่านี้ในงานวิจัยบ้าง ก็เลยคิดว่า ความรู้ที่พอมีอยู่นี้อาจเป็นประโยชน์ต่อการทำงานวิจัยที่อาศัยการคำนวณทางสถิติทั่วไปที่ไม่ลึกนักได้บ้าง ซึ่งน่าจะช่วยได้ในการทำ R2R ส่วนการวิเคราะห์สถิติแบบก้าวหน้า หรือการใช้สถิติสำหรับการวิเคราะห์เฉพาะทางนั้น คงต้องปรึกษาผู้เชี่ยวชาญด้านนี้ต่อไป
![]()
- สวัสดีค่ะ คุณไมโต เห็นช้างไชโยไหมคะ ครูอ้อยทำสำเร็จแล้ว ไชโย คุณไมโตล้อหล่อ ไชโย
- นำเสนองานเป็นอย่างไรบ้างคะ เรียบร้อยญี่ปุ่น ใช่ไหมคะ
- คุณไมโตอยู่แล้ว สบายค่ะ ตามอ่านบันทึกครูอ้อยให้ครบนะคะ ขอบคุณค่ะ จะไปดูรถกระจกใหม่ก่อน ห้าพันค่ะ
- ผ่านไปด้วยดีครับ สำหรับการนำเสนอความก้าวหน้า (ไม่กล้าใช้ความคืบหน้าแล้วล่ะซิ กลัวจะไปได้ทีละคืบ) มีการซักในรายละเอียดบ้าง แต่ก็ไปได้ด้วยบรรยากาศที่ดี
- ตามไปอ่านบันทึกใหม่ของครูอ้อยแล้วครับ ทิ้งรอยไว้แล้วด้วย
- ยินดีด้วยครับครูอ้อย กับเจ้าปิย๊อช(กระจกหลัง)ใหม่
- อีกไม่เกินครึ่งชั่วโมงวันนี้ก็จะได้รู้แล้วครับ ว่าผมจะมีข่าวดีในรอบ 3 อาทิตย์ที่มาอยู่ที่นี่หรือเปล่า
-
 ครูไมโต ดีใจด้วยนะคะที่งานผ่านและได้รู้ความก้าวหน้า ดีใจจริงๆกับความสำเร็จเพื่อคอเดียวกัน
ครูไมโต ดีใจด้วยนะคะที่งานผ่านและได้รู้ความก้าวหน้า ดีใจจริงๆกับความสำเร็จเพื่อคอเดียวกัน - เจ้าปิย๊อชสง่างามเหมือนเดิมเพราะพ่อบ้านเช็ดใหม่เอี่ยมหลังจากปล่อยให้ครูอ้อยลุยมา 3 เดือนแล้ว
- บันทึกของครูอ้อยตั้งมากที่เขียนวันนี้ อ่านหมดแล้วจริงหรือคะ อ่านที่นี่ ที่นี่ และที่นี่ หรือยังคะ
- ขอบคุณค่ะ กินส้มตำใส่ไข่เค็มเผื่อคุณไมโตด้วยค่ะ
- ครูอ้อยครับ ข่าวดีของผมในวันนี้ ก็คือ เมื่อผมตื่นขึ้นมาตอนเช้ากลางทะเล แล้วพบว่าวันนี้อากาศแจ่มใส มองออกไปไกลๆ เห็นฝั่งอยู่ลิบๆ ทำให้มีกำลังใจและรู้ทิศทางที่จะไปให้ถึงฝั่ง แต่จะไปได้ถึงฝั่งจริงหรือเปล่ายังอีกนานครับ แต่ก็ดีว่ามองไปทางไหนก็เห็นแต่น้ำกับฟ้า
- ท่าทางเจ้าปิย๊อชของครูอ้อย ก็คงจะเหมือนกับน้องโตของผม ที่มีชื่อคุณสมจินตนาเป็นเจ้าของ ส่วนผมก็เป็นคนขับ แล้วก็ดูแลเช็ดถู พร้อมกับทำตามคำสั่งครับ วันนี้จะให้ไปส่งที่ไหน ขอให้บอกครับเจ้านาย!
- เพิ่งกลับมาถึงบ้าน เดี๋ยวจะไปตามอ่านให้หมดครับ เรื่องอย่างนี้บ่มียั่น
- เพราะครูอ้อยกินส้มตำไข่เค็มเผื่อนี่เอง ผมถึงรู้สึกอิ่มตื้อๆ อย่างไรไม่รู้ ไปตักแกงเขียวหวานสี่ร้อยปีพร้อมกับไข่เจียวอีกฟอง แล้วรู้สึกเหมือนกินไม่ค่อยลงแล้วล่ะครับ
หลงเข้ามาค่ะ พอดีกำลังหาข้อมูลเกี่ยวกับการวิเคราะห์ข้อมูลด้วยไคว์สแควร์ ไม่กล้าไปหาที่ปรึกษาบ่อยเลยต้องเรียนด้วยตัวเอง ขอบคุณมากสำหรับเนื้อหาดีๆ ขอเรียนรู้ด้วยคนนะคะ ได้รู้เรื่องกว่าเดิมเยอะเลย หัดใช้ spss เองด้วย ประมวลผลออกมาได้ตารางแต่ไม่ค่อยเข้าใจ ได้มาอ่านวันนี้กระจ่างเลยค่ะ ขอบคุณมากค่ะ
หวัดดีค่ะคุณmitocondria อ่านเรื่องที่คุณอธิบายแล้วมีประโยชน์มากมายแต่ยังงงๆอยู่ค่ะ เลยจะขอเรียนถามว่าถ้าดิฉันต้องการจะคำนวนหาว่า คนไข้ที่ติดเชื้อ HIV 292 CASE ติดเชื้อฉวยโอกาส tb 49 case dead 9 case (เหลือไม่dead 40) และมีเชื้อฉวยโอกาสตัวอื่นๆอีกหลายตัว จะใช้ fisher แต่ลองทำใน spss แล้วไม่ได้เลยค่ะ ขอความกรณาชี้แนะให้ด้วยค่ะ ขอด่วนเลยได้ไหมค่ะ จะรบกวนมากไปหรือเปล่า แต่ยังไงก็ขอขอบคุณล่วงหน้าค่ะ