เรียนสถิติด้วยภาพ ตอนที่ 9 การเปรียบเทียบความแตกต่างของค่าเฉลี่ยหลายกลุ่มโดย ANOVA

ANOVA มาจากคำว่า Analysis of Variance คำถามคือ ทำไม variance จึงเปรียบเทียบค่าเฉลี่ยหลายกลุ่มได้ ?

ANOVA มาจากคำว่า Analysis of Variance แต่มาใช้เปรียบเทียบค่าเฉลี่ยของกรณีที่มีหลายกลุ่มพร้อม ๆ กัน

คำถามคือ ทำไม variance จึงเปรียบเทียบค่าเฉลี่ยหลายกลุ่มได้ ? ทำไมไม่ใช้ค่าเฉลี่ยมาเทียบค่าเฉลี่ย ?

เหตุผลที่ไม่เปรียบเทียบค่าเฉลี่ยโดยตรงตั้งแต่ต้น ผมเชื่อว่ามาจากสองเหตุผล

เหตุผลแรก ถ้าเปรียบเทียบค่าเฉลี่ยทุกรายการ ก็ต้องเปรียบไขว้แบบพบกันหมด ซึ่งต้องทำกันมือหงิก

เหตุผลที่สอง วิธีคิดนี้ เกิดมาในยุคที่เครื่องคิดเลขยังไม่แพร่หลาย ต้นทุนคำนวณสูงมาก หากใช้ ANOVA ตอบคำถามด่านแรกได้ว่า จำเป็นไหม ที่จะต้องจับคู่เปรียบเทียบทุกกลุ่ม ถ้าพบว่าไม่จำเป็น ก็ไม่ต้องไปเสียเวลาต่อ เป็นการประหยัดการคำนวณ

ทุกวันนี้ ยังจำเป็นต้องทำ ANOVA ไหม เพราะคอมพิวเตอร์ช่วยคำนวณให้แล้ว ความเห็นผมเองคือ ทำก็ดี เพราะมันทำให้เรากวาดทิ้งกรณีที่ค่าเฉลี่ยเหมือนกันหมดทุกกลุ่มไปได้รวดเดียว โดยไม่ต้องดูทีละคู่ให้เสียเวลา ก็ถือว่ายังมีประโยชน์อยู่ เพราะช่วยประหยัดการตีความ

ตรงนี้แหละ ที่เป็นเรื่องของการพลิกแพลงใช้มุมมองที่ฉลาด มาช่วย โดยนำเรื่อง variance มาใช้เปรียบเทียบค่าเฉลี่ย

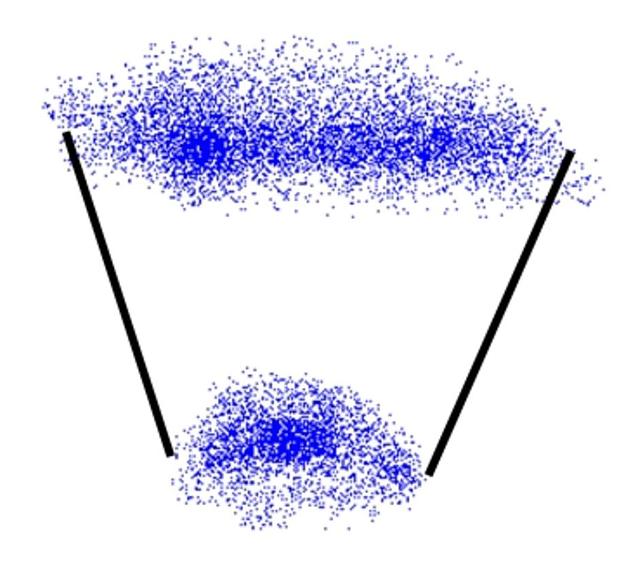
วิธีคิดก็คือ ถ้าค่าเฉลี่ยหลาย ๆ กลุ่ม เหมือนกันจริง ก็เหมือนเราเอาชุมชนแต่ละกลุ่ม มาลองพล็อตตำแหน่งซ้อนกันบนแผนที่ ถ้าทุกกลุ่มเหมือนกันจริง ก็จะซ้อนกันสนิท การซ้อนกันสนิทก็แปลว่า มีจุดร่วมกันที่ศูนย์กลาง

พูดง่าย ๆ ก็คือ เหมือนการใช้เมืองหลวงร่วมกัน โดยเมืองหลวง ก็คือศูนย์กลางที่ทำให้ต้นทุนการเดินทางไปยังจุดย่อย ๆ ของข้อมูลดิบ มีค่าต่ำสุด (ดูตอนก่อนหน้า) ซึ่งต้นทุนที่ว่า ก็คือ variance ซึ่งบอกถึงการกระเจิงรอบศูนย์กลางนั่นเอง



สามรูปนี้ รูปขวาสุด กระเจิงรอบศูนย์กลางที่แท้จริง แต่สองรูปแรก ไม่ใช่ ดังนั้น รูปสุดท้ายนี้ จุดกลาง ก็คือ ค่าเฉลี่ย และการกระเจิงรอบ ๆ รุนแรงไหม ก็คือ variance

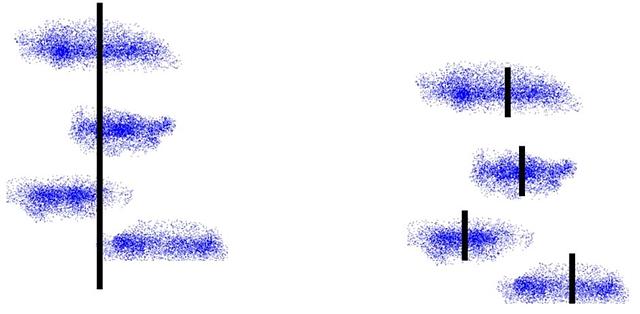
คราวนี้ สมมติว่าเรามีกลุ่มข้อมูลหลายกลุ่ม ที่เราอยากรู้ว่า มันเหมือนกันไหม หรือพูดง่าย ๆ มันซ้อนทับกันเองได้ไหม

รูปซ้าย คือถ้ามันซ้อนทับกันได้จริง มันก็มีศูนย์กลางร่วมกัน (คือเส้นทึบยาว)

รูปขวาคือ ถ้ามันซ้อนกันไม่ได้ มันก็ไม่สามารถมีศูนย์กลางเดียวกัน ต่างก็จะต้องแยกย้ายกันสร้างศูนย์กลางของตัวเอง (เส้นทึบท่อนสั้น)

ANOVA ก็ใช้หลักคิดว่า ถ้าเราคละข้อมูลทุกกลุ่ม แล้วลองดูว่า variance ของการใช้จุดศูนย์กลางร่วมกันหมด (รูปซ้าย) กับการที่ใช้ variance ของกลุ่มใครกลุ่มมัน (รูปขวา) จะทำให้ variance ทั้งสองกรณี เทียบเคียงกันได้ไหม

ถ้า variance ทั้งสองกรณีเทียบเคียงกันได้ คือพอ ๆ กัน ก็แสดงว่า เราจะใช้แบบไหนก็ได้ ซ้ายก็ได้ ขวาก็ดี ก็จะให้ผลเหมือน ๆ กัน

ซึ่งหากถ้าเป็นอย่างนั้น ก็แสดงว่า ใช้ค่าเฉลี่ยค่าเดียวก็ให้ผลเหมือนใช้ค่าเฉลี่ยกลุ่มใครกลุ่มมัน

หรืออีกนัยหนึ่ง เราก็พูดได้ว่า ค่าเฉลี่ยทุกกลุ่ม เหมือนกันหมด คืออยู่ที่เดียวกันนั่นเอง

การเปรียบเทียบ ANOVA ใช้การคำนวณที่เรียกว่า F-test ดังนั้น เวลาทำ ANOVA จึงมีการคำนวณค่า F-test ร่วมด้วยเสมอ

การทำ F-test คือการเทียบว่า แต่ละกรณีมี variance ที่ปรับแก้ผลจากจำนวนประชากรแล้ว พอฟัดพอเหวี่ยงกันไหม

F-test ที่มีนัยสำคัญทางสถิติ แสดงว่า variance ที่มาเปรียบเทียบกันนั้น มันต่างกันเกินไป

ดังนั้น เมื่อทำ ANOVA เราจึงเปรียบเทียบค่า variance ของสองแนวคิด (แนวคิดแรก ใช้ค่าเฉลี่ยร่วมกัน แนวคิดสอง ใช้ค่าเฉลี่ยแยกกัน) ถ้าสถิติบอกว่า ไม่ต่างกัน ก็แสดงว่า เราจะโง่ไปใช้ค่าเฉลี่ยกลุ่มเล็กกลุ่มน้อยทำไมล่ะ เพราะในเมื่อมันก็เหมือนกรณีที่เราใช้ค่าเฉลี่ยค่าเดียว เป็นตัวแทนของทุกกลุ่มได้

หาก ANOVA บอกว่า variance สองกรณีไม่ต่างกัน เราก็สรุปว่า ค่าเฉลี่ยของทุกกลุ่ม เท่ากันหมด

หรือหาก ANOVA บอกว่า variance สองกรณีไม่เท่ากัน เราก็สรุปว่า ค่าเฉลี่ยของทุกกลุ่ม ไม่เหมือนกัน คือมันมีความแตกต่างกัน

และผลจากการทำ ANOVA ก็จะบอกแค่ว่า ทุกกลุ่ม มีค่าเฉลี่ยเหมือนกันทั้งหมดไหม คือจะรู้แค่ว่า ใช่ หรือไม่ใช่

แต่ ANOVA เอง จะไม่สามารถบอกลึกไปกว่านั้นว่า ตกลงแล้ว กลุ่มไหนซ้อนทับกลุ่มไหน หรือกลุ่มไหน แยกขาดจากกลุ่มไหน

ดังนั้น ถ้าทำ ANOVA แล้วเราสรุปว่า ทุกกลุ่มเหมือนกัน เราก็จบแค่นั้น

หรือหากว่า ANOVA บอกว่า ทุกกลุ่ม ไม่ได้เหมือนกันนะ เราก็ต้องไปใช้วิธีสถิติอื่นต่อ ที่เรียกว่า multiple t-test เพื่อดูแยกแยะว่า แต่ละกลุ่มจับคู่เทียบกัน คู่ไหนผูกติดกันเป็นเนื้อเดียว คู่ไหนฉีกแนว แยกตัวออกขาดจากกลุ่มอื่น

 

สนใจอ่าน เรียนสถิติด้วยภาพ แบบครบทุกตอน เข้าไปที่

http://www.gotoknow.org/posts?tag=เรียนสถิติด้วยภาพ