คณิตศาสตร์การเงิน: การกระจายความเสี่ยง-จำลองสถานการณ์

มาดูกรณีสมมติที่เลียนแบบของจริง ว่าเมื่อเจอราคาผันผวน  ชาวสวนผลไม้จะเป็นอย่างไร โดยมาดูกรณีทำสวนเดี่ยว เปรียบเทียบกับสวนผสมที่หลากหลาย

ตอนนี้ภาคต่อของ คณิตศาสตร์การเงิน: การกระจายความเสี่ยง - กรณีศึกษา  ผมมาทำการจำลองในคอมพิวเตอร์ให้ดู

สมมติว่า ราคาผลไม้ ทุก 5 ปี ราคาแย่มาก 2 ปี ราคาปรกติ 2 ปี และราคาดีมาก 1 ปี คือค่อนไปทางไม่เอื้อให้อยู่ได้ คือมีแย่บ่อยกว่ามีดี 

โดยให้ใช้เกณฑ์เทียบราคาว่า

1 คือราคาปรกติ

3 คือราคาดีมาก

0.333 คือราคาแย่มาก

ถ้าหากชาวสวนปลูกผลไม้เพียงชนิดเดียว และลองแจกแจงความถี่ดู จากราคาต่ำไปสูง ก็จะเห็นตัวเลขความเป็นไปได้ว่า จะเจอแบบนั้นมากน้อยแค่ไหน

ผมลองทำ computer simulation ดู ให้ computer สุ่มราคาตามข้อสมมติ โดยให้ลองทำดู 1 แสนครั้ง แล้วลองแจกแจงความถี่ (ดูตัวเลขข้อมูลดิบจากข้างล่าง) ตัวเลขจะกระเพื่อมนิดหน่อย เพราะใช้วิธีสุ่มหยิบตามข้อสมมติข้างต้น

ลองดูกรณีแรก คือสวนเดี่ยว

ผมไม่ทำกราฟ บรรยายเอาตรง ๆ 

กรณีนี้สวนผลไม้เดี่ยว มีโอกาสขาดทุนหนัก 40 % และมีโอกาสกำไรดีมาก 20 % ตรงตามข้อสมมติข้างต้น ซึ่งอาจถือว่า มีแนวโน้มค่อนไปทางราคาไม่ดี (ดูจากตารางตัวเลขในภาคผนวกนะครับ)

หากทำเป็นสวนผสมแบบคู่ 2 ชนิดล่ะ

 

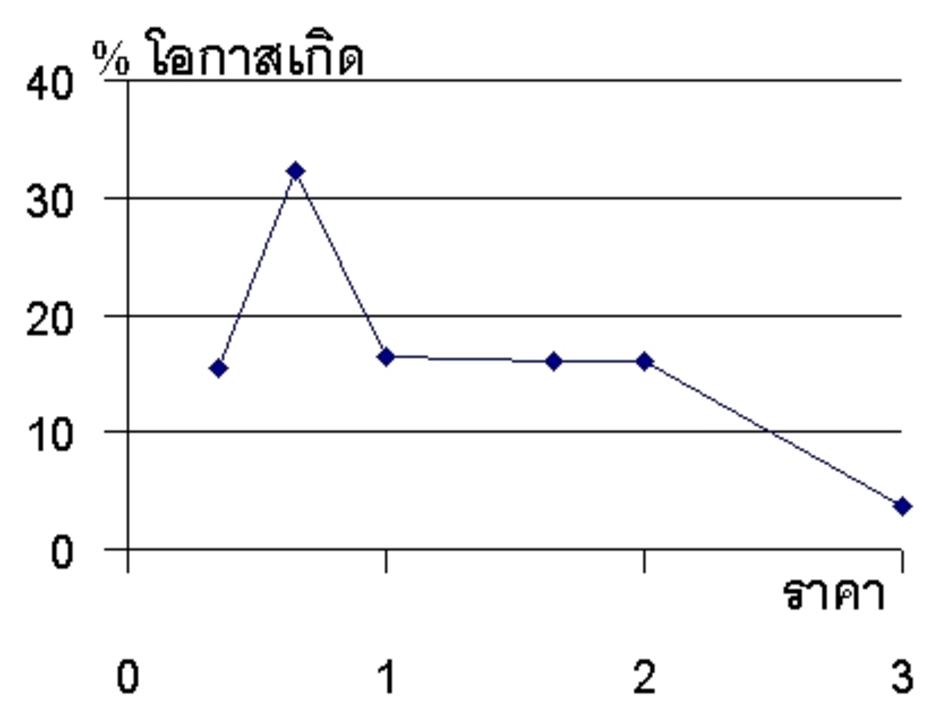
กรณีสวนผลไม้ผสม 2 ชนิด มีโอกาสขาดทุนหนัก 16 % ขาดทุนปานกลาง 32 % โดยกราฟจะถ่วงไปทางซ้ายมาก คือราคาไม่ดีบ่อย

ถ้าผสม 3 ชนิดล่ะ ?

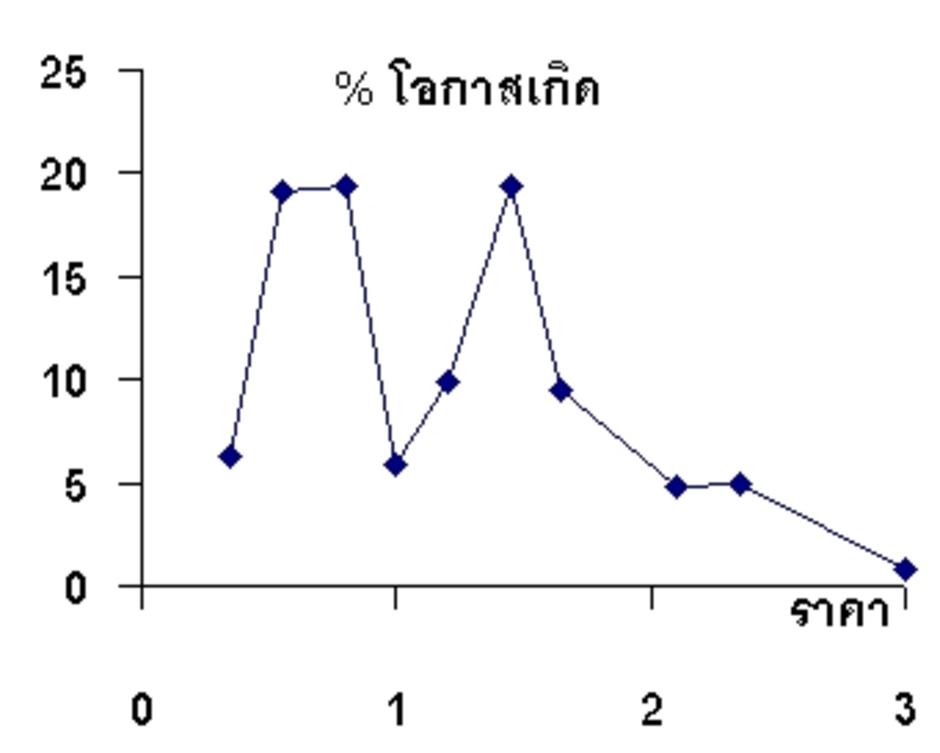
รูปกราฟดูพิลึก ๆ หน่อยนะครับ แต่ในกรณีนี้ผมจำลองสถานการณ์ตั้งแสนครั้ง ค่าที่ได้ ค่อนข้างนิ่งแล้ว ทำมากกว่านี้ก็ไม่น่าจะต่างออกไป อันที่จริง ทำเพียงหมื่นครั้งก็เห็นแบบนี้เหมือนกัน  

กรณีผสม 3 ชนิด มีโอกาสขาดทุนหนัก 6 % ขาดทุนปานกลาง 38 %

กรณีผสม 2 หรือ 3 ชนิด ก็เหมือนคนที่ป่วยเบา ๆ บ่อยขึ้น แต่ลดการล้มหมอนนอนเสื่อลง

 

ถ้าผสม 5 ชนิดล่ะ

 

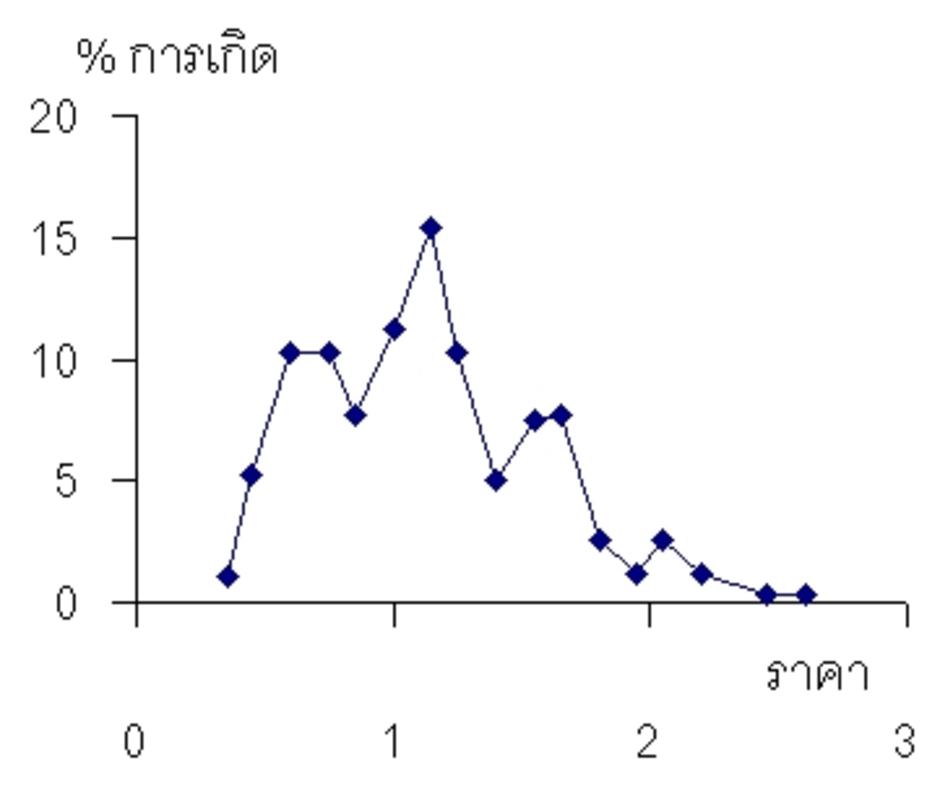
โอกาสขาดทุนหนักมาก ก็ยังอยู่คล้ายเดิม คือราว 6 % และขาดทุนปานกลางราว 25 %

ทีนี้ ถ้าผสม 10 ชนิดล่ะ 

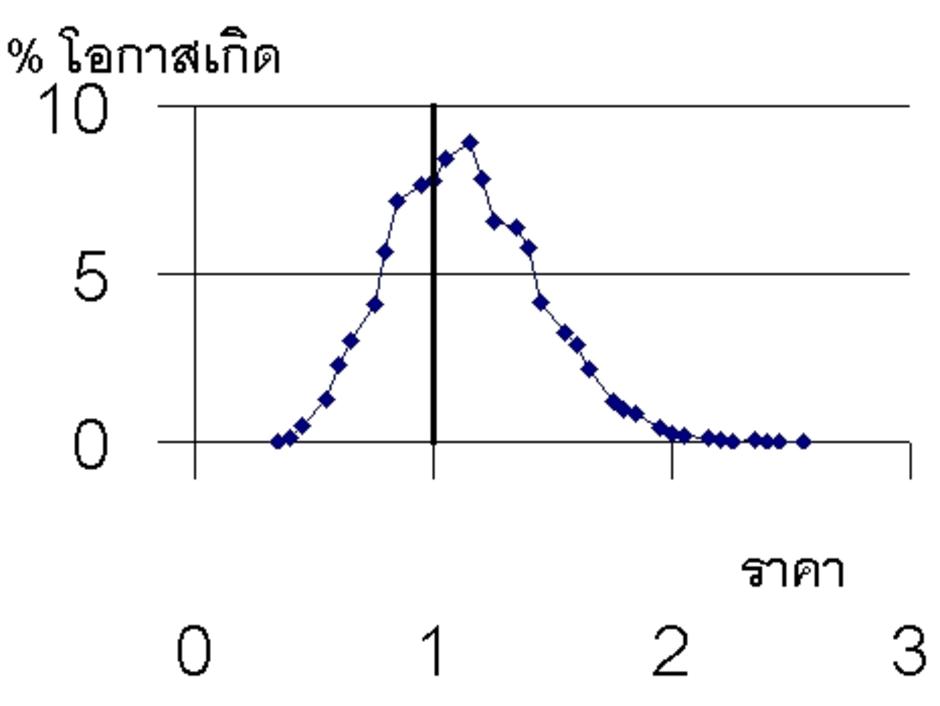
ถ้าดูกราฟ จะเห็นว่า ถ่วงไปทางขวา (ราคาดีปานกลางเป็นส่วนใหญ่) มากกว่าครึ่ง ทั้งที่สภาวะเริ่มต้นที่เรากำหนดไว้คือ ผลไม้เดี่ยว มีโอกาสเกิดราคาแย่มากสูงถึง 40 % ซึ่งจะทำให้กราฟตั้งต้น ถ่วงไปทางซ้าย

ในกรณีนี้ จะขาดทุนหนักมากเหลือราว 2 % แต่ขาดทุนปานกลางก็นิ่งอยู่ที่ราว 30 %

 

 

ดูอีกแบบหนึ่งก็ได้ คือดูเป็นช่วงความเชื่อมั่นแทน

ดูแบบนี้ อาศัยหลักว่า ตัดค่าหัวท้ายที่รุนแรงออก ทำให้เห็นก้อนรวมที่ลอกเปลือกขรุขระออกแล้ว ซึ่งจะมีค่าที่ "กลมเกลี้ยง" ขึ้น เห็นชัดขึ้น หยิบจับง่ายขึ้น

ผสมกี่ชนิด	ค่าล่างความเชื่อมั่น 90 %	ค่ามัธยฐาน	ค่าบนความเชื่อมั่น 90 %
1	.35	1	3
2	.35	1	2
3	.35	1	2.35
5	.45	1.15	1.95
10	.65	1.15	1.65

อาจดูช่วงความเชื่อมั่น 90 % ก็ได้ คือ ตัดค่าที่สูงสุด 5 % แรก และค่าต่ำสุด 5 % แรก ทิ้งออกไป โดยถือว่าเป็นพวกสุดโต่ง ก็จะเป็นภาพใหญ่ของปรากฎการณ์ที่เห็นชัดเจนขึ้น คือกรณีทั่วไป จะเกิดตามกรอบนี้ หายากที่จะหลุดออกไป ก็จะเห็นได้ชัดว่า เมื่อเพิ่มความหลากหลาย การขาดทุนรุนแรง-กำไรรุนแรง จะหายไปจากสารบบ

มัธยฐานก็คือ เส้นที่แบ่งครึ่งข้อมูล มีข้อมูลครึ่งหนึ่งที่ต่ำกว่านี้ และข้อมูลอีกครึ่งหนึ่ง จะอยู่สูงกว่านี้ 

ตามปรกติแล้ว หากมีข้อมูลแปลก ๆ ที่ไม่รู้พฤติกรรม มัธยฐาน จะเป็นตัวชี้วัดองค์รวมที่ปลอดภัยที่สุดในการใช้งาน ปลอดภัยกว่าค่าเฉลี่ย เพราะต่อให้มีข้อมูลขยะติดปนมาบ้าง มัธยฐานก็ไม่กระดิก

ก็จะเห็นได้ว่า ความหลากหลาย ช่วยได้จริง เพราะค่ามัธยฐานกระเถิบสูงขึ้น

ข้อสรุปก็คือ ยิ่งทำสวนผสมให้หลากหลายมากขึ้น กรณีที่ราคาแย่มาก ก็ไม่ค่อยเจอ โอกาสรวยมากก็ไม่ค่อยเจอเหมือนกัน แต่เจอราคาเฉลี่ยดีปานกลางบ่อยขึ้นมาก

เป็นการเฉลี่ยทุกข์-เฉลี่ยสุข โดยความสุข เกิดบ่อยขึ้น เกิดในระดับสบาย ๆ ค่อนข้างแน่นอน ไม่หวือหวา ไม่ต้องลุ้นระทึกเรื่องราคามาก

ขอเพียงแต่ละปี มีบางรายการที่ราคาดีมากผิดคาดสักรายการเดียว หรือค่อนข้างดีมากกว่าหนึ่งรายการเกิดพร้อมกัน ก็พออยู่ได้แล้ว

นี่คือพลังของการกระจายความเสี่ยงครับ

 

ป.ล. แต่ยังต้องลุ้นระทึกเรื่องภัยพิบัติจากธรรมชาติอยู่นะครับ เพราะที่ว่ามา กระจายความเสี่ยงในมิติของราคาเรื่องเดียว ไม่ได้กระจายความเสี่ยงเชิงภูมิศาสตร์