ตารางเมทริกซ์สหสัมพันธ์ (Correlation matrix) คืออะไร
ตารางเมทริกซ์สหสัมพันธ์ (Correlation matrix)
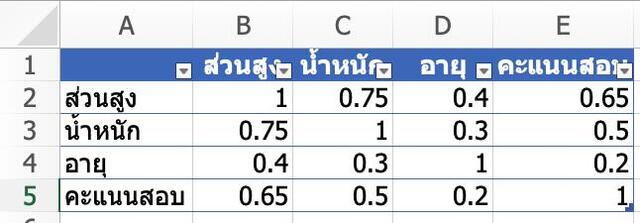
ตารางเมทริกซ์สหสัมพันธ์ (Correlation matrix) นี้มีตัวแปรสี่ตัว ได้แก่ ส่วนสูง น้ำหนัก อายุ และคะแนนสอบ และแต่ละเซลล์ในตารางแสดงค่าสัมประสิทธิ์สหสัมพันธ์ระหว่างตัวแปรสองตัว
การแปลผลตารางค่าสัมประสิทธิ์สหสัมพันธ์
- เซลล์ที่จุดตัดของส่วนสูงและน้ำหนักแสดงค่าสัมประสิทธิ์สหสัมพันธ์เท่ากับ 0.75 แสดงให้เห็นความสัมพันธ์เชิงบวกที่แข็งแกร่งระหว่างส่วนสูงและน้ำหนัก เมื่อความสูงเพิ่มขึ้น น้ำหนักก็มีแนวโน้มเพิ่มขึ้นเช่นกัน
- เซลล์ที่จุดตัดของส่วนสูงและอายุแสดงค่าสัมประสิทธิ์สหสัมพันธ์เท่ากับ 0.40 บ่งบอกถึงความสัมพันธ์เชิงบวกในระดับปานกลางระหว่างส่วนสูงและอายุ โดยเฉลี่ยแล้ว คนที่สูงมักจะแก่กว่า แต่ความสัมพันธ์ไม่แข็งแรงเท่ากับน้ำหนัก
- เซลล์ที่จุดตัดของส่วนสูงและคะแนนสอบแสดงค่าสัมประสิทธิ์สหสัมพันธ์เท่ากับ 0.65 บ่งชี้ความสัมพันธ์เชิงบวกในระดับปานกลางระหว่างส่วนสูงและคะแนนสอบ แสดงให้เห็นว่าโดยเฉลี่ยแล้ว นักเรียนที่ตัวสูงมักจะได้คะแนนสอบสูงกว่า
- เซลล์ที่จุดตัดของน้ำหนักและอายุแสดงค่าสัมประสิทธิ์สหสัมพันธ์เท่ากับ 0.30 ชี้ให้เห็นถึงความสัมพันธ์เชิงบวกที่อ่อนแอระหว่างน้ำหนักและอายุ บ่งชี้ว่า โดยเฉลี่ยแล้ว คนมีอายุมากขึ้นมักจะมีน้ำหนักเพิ่มขึ้นเล็กน้อย
- เซลล์ที่จุดตัดของน้ำหนักและคะแนนสอบแสดงค่าสัมประสิทธิ์สหสัมพันธ์เท่ากับ 0.50 แสดงให้เห็นความสัมพันธ์เชิงบวกในระดับปานกลางระหว่างน้ำหนักและคะแนนสอบ แสดงว่าโดยเฉลี่ยแล้ว นักเรียนที่มีน้ำหนักมากกว่ามักจะได้คะแนนสอบสูงกว่า
- เซลล์ที่จุดตัดของอายุและคะแนนสอบแสดงค่าสัมประสิทธิ์สหสัมพันธ์เท่ากับ 0.20 บ่งบอกถึงความสัมพันธ์เชิงบวกที่อ่อนแอระหว่างอายุและคะแนนสอบ โดยเฉลี่ยแล้ว นักเรียนที่มีอายุมากกว่ามักจะมีคะแนนสอบสูงกว่าเล็กน้อย แต่ความสัมพันธ์ไม่แน่นแฟ้นมากนัก
ความเห็น (1)
May I add supplementary materials and an often omitted point that the correlation matrix is useful only when the data (of 2+ variables) is ‘normally distributed’ – like many other ‘common’ statistical tests. Thus before we go into correlation matrix we have to assure that ‘normal distribution’ is tested.
A guide to appropriate use of Correlation coefficient in medical Research https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3576830/
–In summary, correlation coefficients are used to assess the strength and direction of the linear relationships between pairs of variables. When both variables are normally distributed use Pearson’s correlation coefficient, otherwise use Spearman’s correlation coefficient.
Chapter 22: Correlation Types and When to Use Them https://ademos.people.uic.edu/Chapter22.html
Should I use Pearson or Spearman or Kendall? [Emphasis: Assuption 4]–We can see Pearson and Spearman are roughly the same, but Kendall is very much different. That’s because Kendall is a test of strength of dependency (i.e. one could be written as a linear function of the other), whereas Pearson and Spearman are nearly equivalent in the way they correlate ‘normally distributed ‘ data.