โครงงานกลุ่มสาระการเรียนรู้คณิตศาสตร์
เรื่อง คณิตศาสตร์กับลักษณะการเดินของนาฬิกา
หน้า 1
บทคัดย่อ
จากโครงงานคณิตศาสตร์กับลักษณะการเดินของนาฬิกาได้ดำเนินการโดยมีจุดมุ่งหมายเพื่อที่จะศึกษาวิธีการดำเนินการทางคณิตศาสตร์กับลักษณะการเดินของนาฬิกา แล้วนำผลที่ได้ไปสร้างจัตุรัสรูปแบบต่าง ๆ ที่เกิดจากการกำหนดสีของเลขโดดแต่ละจำนวน หลังจากนั้นได้ศึกษารูปแบบที่เปลี่ยนไปของการหมุนหรือการพลิกตารางจัตุรัส แล้วนำรูปแบบที่ได้ไปประยุกต์ใช้ในการสร้างรูปแบบลวดลายใหม่ที่สวยงาม
การดำเนินการเริ่มจากการร่วมกันคิด วิเคราะห์ วางแผน และตัดสินในเลือกเรื่องที่จะทำ แล้วมีการแบ่งงานไปศึกษาหาข้อมูล และดำเนินการศึกษาในหัวข้อที่ได้รับมอบหมาย หลังจากนั้นนำผลการศึกษาที่ได้มาสรุป วิเคราะห์ แล้วเรียบเรียงเป็นรูปเล่มรายงาน
ผลจากการศึกษาพลว่า วิธีดำเนินการทางคณิตศาสตร์มีความเกี่ยวข้อกับลักษณะการเดนของนาฬิกา สามารถนำผลจากการศึกษาไปสร้างตารางจัตุรัสในรูปแบบต่าง ๆ ที่เกิดจากการกำหนดสีของเลขโดแต่ละจำนวนได้ เมื่อนำมาหมุนหรือพลิกตารางจัตุรัส จากการดำเนินการศึกษาทั้งหมด 8 รูปแบบ พบว่าจะได้รูปแบบเปลี่ยนไป 4 รูปแบบ และเมื่อนำรูปแบบนั้นมาผสมผสารสามารถสร้างลวดลายใหม่ตามความสนใจได้อีกมากมาย
คำนำ
การเรียนการสอนวิชาคณิตศาสตร์ที่มุ่งเน้นให้ผู้เรียนมีความรู้ในวิชาคณิตศาสตร์จากการเรียนในห้องเพียงอย่างเดียวทำให้นักเรียนมีความคิดเกี่ยวกับวิชาคณิตศาสตร์ว่าวิชาคณิตศาสตร์เป็นวิชาที่ต้องเน้นทฤษฎี หลักการ และเนื้อหาเท่านั้น ซึ่งมีผลทำให้นักเรียนไม่ชอบวิชาคณิตศาสตร์
ในการจัดทำโครงงานนี้เป็นการใช้คณิตศาสตร์ขั้นพื้นฐานในการทำโครงงานเป็นการผสมผสานวิชาคณิตศาสตร์ กระบวนการคิด การจัดการอย่างสมดุล กับหลักการอื่น ๆ เข้าด้วยกันทำให้เกิดสิ่งที่แปลกใหม่ น่าสนใจ และน่าที่จะศึกษาค้นคว้า ตลอดจนส่งเสริมให้นักเรียนรู้จักคิดวิเคราะห์ วางแผน นำสิ่งรอบตัวมาประยุกต์เข้ากับการเรียนในวิชาคณิตศาสตร์ ซึ่งโครงงานที่จัดทำขึ้นนี้ได้อาศัยหลักการเดินของเข็มนาฬิกา แต่เมื่อเรานำมาคิด วิเคราะห์ และดัดแปลง จึงเกิดความรู้และได้รับประสบการณ์ที่แปลกใหม่
ผู้จัดทำหวังว่า โครงงานคณิตศาสตร์นี้จะเป็นประโยชน์ต่อผู้ที่สนใจวิชาคณิตศาสตร์ และผู้ที่ต้องการจะศึกษาค้นคว้าทุก ๆ ท่าน ขอขอบพระอาจารย์ประสิทธิ์ มายูร ที่ช่วยเป็นที่ปรึกษาและดูแลเป็นอย่างดี
คณะผู้จัดทำ
สารบัญ
ที่มาและความสำคัญของโครงงาน
วัตถุประสงค์
วิธีการดำเนินงาน
การศึกษาข้อมูลพื้นฐานก่อนออกแบบหรือกำหนดแนวทาง
สมมุติฐาน
สรุปผลการศึกษาหรือผลงานที่เกิดขึ้น
แนวทางการนำผลไปใช้ การอภิปรายผล และข้อเสนอแนะ
บรรณานุกรม
หน้า
6
6
7
7
8
18
ที่มาและความสำคัญของโครงงาน
ในการดำเนินชีวิตประจำวันเรามีความเกี่ยวข้องกับเวลาอยู่ตลอดไม่ว่าเราจะทำกิจกรรมใด ๆ เช่น 06.00 น. ตื่นนอน 06.30 – 07.30 น. อาบน้ำ เป็นต้น
นาฬิกาเป็นเครื่องมือสำคัญที่ใช้ในการบอกเวลาซึ่งในนาฬิกานั้นมีการนำตัวเลขต่าง ๆ เข้าไปเกี่ยวข้อง ได้แก่ เลข 1 ถึงเลข 12 เมื่อเราได้พิจารณาลักษณะการเดินของนาฬิกา ซึ่งมีทั้งการเดินตามเข็มนาฬิกาเป็นการเดินจากขวาไปซ้าย หรือจากเลข 1,2 ไปยังเลข 12 และการเดินทวนเข็มนาฬิกาเป็นการเดินจากซ้ายไปขวา หรือจากเลข 12,11 ย้อนไปยังเลข 1 และยับได้พบสมบัติอย่างหนึ่งของการเดินของนาฬิกาจะเริ่มเดินจากเลข 1 ไปเลข 2 ไปจนถึงเลข 12 เป็นเช่นนี้ซ้ำแล้วซ้ำอีก จากลักษณะการเดินของนาฬิกาดังกล่าวทำให้สามารถนำมาสร้างตารางจัตุรัสเพื่อศึกษาความเกี่ยวข้องทางคณิตศาสตร์ได้ ด้วยเหตุนี้ทางกลุ่มเราจึงสนใจที่จุศึกษาความเกี่ยวข้องของคณิตศาสตร์กับลักษณะการเดินของนาฬิกา
วัตถุประสงค์
1. เพื่อศึกษาวิธีการดำเนินการทางคณิตศาสตร์กับลักษณะการเดินของนาฬิกา
2. เพื่อนำผลจากวิธีการดำเนินการทางคณิตศาสตร์ตามลักษณะการเดินของนาฬิกาไปสร้างตารางจัตุรัสรูปแบบต่าง ๆ ที่เกิดจากการกำหนดสีของเลขโดดแต่ละจำนวน
3. ศึกษารูปแบบที่เปลี่ยนไปของการหมุนหรือการพลิกตารางจัตุรัสที่ได้จากการดำเนินการทางคณิตศาสตร์ตามลักษณะการเดินของนาฬิกา
4. เพื่อสร้างลวดลายต่าง ๆ ที่ได้จากการผสมผสานรูปแบบต่าง ๆ ของการดำเนินการทางคณิตศาสตร์ตามลักษณะการเดินของนาฬิกา
วิธีการดำเนินงาน
1. จัดตั้งกลุ่มโครงงาน ซึ่งประกอบด้วยสมาชิก 9 คน ได้มีการประชุมปรึกษาหารือเกี่ยวกับการดำเนินการจัดทำโครงงาน โดยกลุ่มได้แบ่งหน้าที่ให้สมาชิกออกไปศึกษาข้อมูลเอกสารต่าง ๆ
2. ประชุมปรึกษาหารือในการหาหัวข้อของโครงงานคณิตศาสตร์ที่กลุ่มจะดำเนินการ โดยทางกลุ่มได้มีการเสนอหัวข้อที่จะดำเนินการหลายอย่าง เช่น ลักษณะของการผสมสี ลักษณะการหมุนของนาฬิกา เป็นต้น ซึ่งทางกลุ่มเห็นว่าลักษณะของการหมุนของนาฬิกาเป็นเรื่องที่น่าสนใจจึงได้ตกลงที่จะทำการศึกษา ลักษณะการหมุนของนาฬิกา ซึ่งทางกลุ่มได้กลับไปศึกษาเอกสารต่าง ๆ ที่เกี่ยวข้องอีกครั้ง
3. ประชุมปรึกษาหารือ ร่วมกันวิเคราะห์วางแผน แล้วกำหนดแนวทางในการดำเนินงาน
4. ดำเนินการศึกษาวิธีดำเนินกาทางคณิตศาสตร์กับลักษณะการเดินของนาฬิกา แล้วนำผลที่ได้ไปสร้างตารางจัตุรัสรูปแบบต่าง ๆ หลังจากนั้นได้ศึกษาการหมุนหรือการพลิกตารางจัตุรัสให้เกิดรูปแบบที่แตกต่างไป และมีการผสมผสานรูปแบบข้างต้น เพื่อสร้างลวดลายต่าง ๆ ที่สวยงาม ซึ่งมีการแบ่งหน้าที่ดำเนินการ
5. สรุปผลจากการดำเนินการ
6. ประชุมอภิปรายปัญหาต่าง ๆ และให้ข้อเสนอแนะ
7. จัดทำรายงานโครงงานคณิตศาสตร์
8. นำเสนอโครงงานคณิตศาสตร์
การศึกษาข้อมูลพื้นฐานก่อนออกแบบหรือกำหนดแนวทาง
ทางกลุ่มได้ศึกษาข้อมูลพื้นฐานก่อนกำหนดแนวทางในการดำเนินงาน ดังนี้
1. ความหมาย หลักการ จุดประสงค์ ประเภท ขั้นตอน และตัวอย่างของการทำโครงงานคณิตศาสตร์
2. ลักษณะการเดินของนาฬิกา
3. ระบบจำนวนจริง ได้แก่ การดำเนินการต่าง ๆ สมบัติของจำนวน เป็นต้น
4. เรขาคณิต ได้แก่ ลักษณะของรูปทางเรขาคณิต การหมุนหรือการพลิกรูปทางเรขอคณิต
สมมุติฐาน
1. วิธีการดำเนินการทางคณิตศาสตร์ มีความเกี่ยวข้องกับลักษณะการเดินของนาฬิกา
2. ผลจากวิธีการดำเนินการทางคณิตศาสตร์ตามลักษณะการเดินของนาฬิกา สามารถสร้างตารางจัตุรัสรูปแบบต่าง ๆ ที่เกิดจากการกำหนดสีของเลขโดดแต่ละจำนวนได้
3. การหมุนหรือการพลิกตารางจัตุรัสที่ได้จากการดำเนินการทางคณิตศาสตร์ตามลักษณะการเดินของนาฬิกาทำให้รูปแบบของตารางจัตุรัสเปลี่ยนไป
4. การผสมผสานรูปแบบต่าง ๆ ของการดำเนินการทางคณิตศาสตร์ ตามลักษณะการเดินของนาฬิกาทำให้เกิดลวดลายต่าง ๆ ได้
สรุปผลการศึกษาหรือผลงานที่เกิดขึ้น
1. ทางกลุ่มได้ศึกษาวิธีการดำเนินการทางคณิตศาสตร์กับลักษณะการเดินของนาฬิกา ดังนี้
1.1 วิธีการดำเนินการทางคณิตศาสตร์
วิธีการดำเนินการทางคณิตศาสตร์ที่กลุ่มได้ศึกษาจากเอกสาร ได้แก่
- การบวก เช่น 2 + 5 = 7 เป็นต้น
- การลบ เช่น 5 - 8 = -3 เป็นต้น
- การคูน เช่น 4 x 5 = 20 เป็นต้น
- การหาร เช่น 10 ÷ 2 = 5 เป็นต้น
1.2 เลขโดด
เลขโดดในระบบตัวเลขฐานต่าง ๆ จะมีจำนวนต่างกันไป เช่น เลขโดดของระบบตัวเลขฐานสิบจะมีเลขโดดอยู่ 10 ตัว ได้แก่ 0,1,2,3,4,5,6,7,8,9 เลขโดดของระบบตัวเลขฐานสองจะมีเลขโดดอยู่ 2 ตัว ได้แก่ 0,1 เป็นต้น
1.3 ลักษณะการเดินของนาฬิกา
ลักษณะการเดินของนาฬิกาซึ่งมีทั้งการเดินตามเมนาฬิกาเป็นการเดินจากขวาไปซ้ายหรือจากเลข 1,2 ไปยัง 12 และการเดินทวนเข็มนาฬิกาเป็นการเดินจากซ้ายไปขวาหรือจากเลข 12,11 ย้อนไปยังเลข 1 และยังได้พบลักษณะอย่างหนึ่งของการเดินของนาฬิกาว่าเข็มของนาฬิกาจะเริ่มเดินจากเลข 1 ไปเลข 2 ไปจนถึงเลข 12 แล้วกลับมาเริ่มเดินจากเลข 1 ไปเลข 2 ไปจนถึงเลข 12 เป็นเช่นนี้เสมอ ๆ
1.4 วิธีการดำเนินการทางคณิตศาสตร์ตามลักษณะการเดินของนาฬิกา
จากลักษณะการเดินของเข็มนาฬิกา ทำให้กลุ่มได้กำหนดวิธีการทางคณิตศาสตร์ตามลักษณะการเดินของนาฬิกาได้ 3 ลักษณะ คือ การบวก การลบ การคูณ โดยจำนวนที่ใช้ดำเนินการต้องทำในรูปแบบของตารางจัตุรัส และเป็นเลขโดด ทางกลุ่มสามารถกำหนดเลขโดดเรียงกันได้หลากหลาย เช่น
- กำหนด 2 ตัว ได้แก่ 0,1 0
- กำหนด 3 ตัว ได้แก่ 0,1,2
- กำหนด 4 ตัว ได้แก่ 0,1,2,3 เป็นต้น 1
ทางกลุ่มเห็นว่าการหารไม่สามารถทำได้ เนื่องจากมีบางจำนวนดำเนินการแล้วได้ผลลัพธ์เป็นเศษส่วน ซึ่งไม่สามารถลงเป็นจำนวนในเลขโดดนั้นได้
ตัวอย่าง การดำเนินการเกี่ยวกับการบวก โดยใช้เลขโดด 0,1,2
+
0
1
2
0
0
1
2
1
1
2
0
2
2
0
1
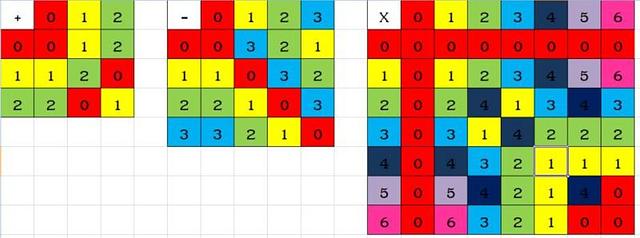
จากตารางจะเห็นว่า ทางกลุ่มใช้วิธีการนำเลขในแต่ละแถว มาบวกกับเลขแต่ละหลักตามวิธีปกติ ถ้าผลบวกที่ได้มีจำนวนเกินกว่าเลขโดดที่มากที่สุดให้นับต่อไปตามลักษณะการหมุนตามเข็มของนาฬิกา เช่น 2 + 2 = 4 ซึ่งมีค่ามากกว่า 2 ซึ่งเป็นเลขโดดที่มีค่ามากที่สุด ให้นับกลับมาที่ 0,1,2 ซ้ำตามรูป จะได้ว่า 2 + 2 มีค่าเท่ากับ 1 ตามวิธีการดำเนินการตามลักษณะการเดินของนาฬิกา
ตัวอย่าง การดำเนินการเกี่ยวกับการลบ โดยใช้เลขโดด 0,1,2,3
-
0
1
2
3
0
0
3
2
1
1
1
0
3
2
2
2
1
0
3
3
3
2
1
0
จากตารางจะเห็นว่าทางกลุ่มใช้วิธีการนำเลขในแต่ละแถว มาลบกับเลขแต่ละหลักตามวิธีการปกติ ถ้าผลลบที่ได้มีค่าที่ติดลบ ให้นับย้อนกลับตามลักษณะการหมุนทวนเข็มของนาฬิกา เช่น 2 - 3 = -1 ซึ่งมีค่าติดลบ ให้นับกลับตามลักษณะการหมุนทวนเข็มของนาฬิกามา 1 ครั้งตามรูป จะได้ว่า 2 - 3 มีค่าเท่ากับ 3
ตัวอย่าง การดำเนินการเกี่ยวกับการคูณ โดยใช้เลขโดด 0,1,2,3,4
X
0
1
2
3
4
0
0
0
0
0
0
1
0
1
2
3
4
2
0
2
4
1
3
3
0
3
1
4
2
4
0
4
3
2
1
จากตารางจะเห็นว่าทางกลุ่มใช้วิธีการนำเลขในแต่ละแถว มาคูณกับตัวเลขในแต่ละหลักตามวิธีการปกติ ถ้าผลคูณที่ได้มีจำนวนเกินกว่าเลขโดดที่มากที่สุด ให้นับต่อไปตามลักษณะการหมุนตามเข็มของนาฬิกา เช่น 2 x 4 = 8 ซึ่งมีค่ามากกว่า 4 ซึ่งเป็นเลขโดดที่มีค่ามากที่สุดให้นับกลับมาที่ 0,1,2 ซ้ำตามรูป จะได้ว่า 2 x 4 มีค่าเท่ากับ 3 ตามวิธีการดำเนินการตามลักษณะการเดินของนาฬิกา
2. ทางกลุ่มได้นำผลจากวิธีการดำเนินการทางคณิตศาสตร์ตามลักษณะการเดินของนาฬิกาไปสร้างตารางจัตุรัสรูปแบบต่าง ๆ ที่เกิดจากการกำหนดสีของเลขโดดแต่ละจำนวน ดังนี้
เลขโดด 0 คือ สีแดง
เลขโดด 1 คือ สีเหลือง
เลขโดด 2 คือ สีเขียว
เลขโดด 3 คือ สีฟ้า
เลขโดด 4 คือ สีน้ำเงิน
เลขโดด 5 คือ สีม่วง
เลขโดด 6 คือ สีชมพู
ตัวอย่าง ตารางจัตุรัสรูปแบบต่าง ๆ ที่เกิดจากการกำหนดสีของเลขโดด 0,1 ของการดำเนินการทางคณิตศาสตร์ ตามลักษณะการเดินของนาฬิกา มีดังนี้
ตัวอย่าง ตารางจัตุรัสรูปแบบต่าง ๆ ที่เกิดจากการกำหนดสีของเลขโดด 0,1,2 ของการดำเนินการทางคณิตศาสตร์ตามลักษณะการเดินของนาฬิกา มีดังนี้
ตัวอย่าง ตารางจัตุรัสรูปแบบต่าง ๆ ที่เกิดจากการกำหนดสีของเลขโดด 0,1,2,3,4,5,6 ของการดำเนินการทางคณิตศาสตร์ตามลักษณะการเดินของนาฬิกา มีดังนี้
จากตัวอย่างข้างต้น จะเห็นว่าทางกลุ่มใช้การดำเนินการ การบวก การลบ และการคูณในแต่ละชุดของเลขโดด ซึ่งทำให้ได้ตารางจัตุรัสรูปแบบต่าง ๆ ที่หลากหลายกันออกไป
3. ทางกลุ่มได้ศึกษารูปแบบที่เปลี่ยนไปโดยได้ตกลงกันว่าจะทำการหมุนหรือการพลิกตารางจัตุรัสที่กำหนดสีแล้ว ที่ได้จากการดำเนินการทางคณิตศาสตร์ตามลักษณะการเดินของนาฬิกาเพื่อที่จะได้รูปแบบที่แปลกใหม่ โดยกำหนดการหมุน และการพลิกตารางจัตุรัสไว้ดังนี้
ตัวอย่าง การหมุนและการพลิกตารางจัตุรัสของดำเนินการโดยการบวกของเลขโดด 0,1,2 จากตารางจัตุรัสของดำเนินการโดยการบวกของเลขโดด 0,1,2
รูปแบบ A ไม่หมุนตารางจัตุรัส
รูปแบบ B การหมุนตารางจัตุรัสเป็นมุม 90 องศา
รูปแบบ C การหมุนตารางจัตุรัสเป็นมุม 180 องศา
รูปแบบ D การหมุนตารางจัตุรัสเป็นมุม 270 องศา
รูปแบบ E การพลิกในแนวตั้ง
รูปแบบ F การพลิกในแนวนอน
รูปแบบ G การพลิกทแยงมุมขวา
รูปแบบ H การพลิกทแยงมุมซ้าย
จากตัวอย่างข้างต้น และการทดลองหมุน หรือพลิกตารางจัตุรัสที่ได้จากการดำเนินการทางคณิตศาสตร์ตามลักษณะการเดินของนาฬิกา ทางกลุ่มเห็นว่าดำเนินการหมุน หรือพลิกได้ 8 แบบ และทางกลุ่มเห็นว่าการพลิกในแนวต่าง ๆ จะมีลักษณะรูปแบบซ้ำกันกับการหมุน ทางกลุ่มจึงตกลงว่าจะศึกษาเฉพาะรูปแบบการหมุนตารางจัตุรัส นั้นคือรูปแบบ A,B,C และ D
ตัวอย่าง การหมุนและการพลิกตารางจัตุรัสของดำเนินการโดยการบวกของเลขโดด 0,1,2,3,
4,5,6
ตารางจัตุรัสของดำเนินการโดยการคูณ ของเลขโดด 0,1,2,3,4,5,6
รูปแบบ A ไม่หมุนตารางจัตุรัส
รูปแบบ B การหมุนตารางจัตุรัสเป็นมุม 90 องศา
รูปแบบ C การหมุนตารางจัตุรัสเป็นมุม 180 องศา
รูปแบบ D การหมุนตารางจัตุรัสเป็นมุม 270 องศา
จากตัวอย่างรูปแบบที่เปลี่ยนไปจากการหมุนหรือพลิกตารางจัตุรัสทีได้จากการดำเนินการทางคณิตศาสตร์ตามลักษณะการเดินของนาฬิกา จะเห็นว่าทางกลุ่มได้รูปแบบที่แตกต่างกันมา 4 รูปแบบ ในแต่ละการดำเนินการทางคณิตศาสตร์ตามลักษณะการเดินของนาฬิกาของชุดเลขโดดต่าง ๆ
4. ทางกลุ่มได้สร้างลวดลายต่าง ๆ ที่ได้จากการผสมผสานรูปแบบต่าง ๆ ของการดำเนินการทางคณิตศาสตร์ตามลักษณะการเดินของนาฬิกา โดยกลุ่มได้นำตารางจัตุรัสมาสร้างลวดลายต่าง ๆ ที่น่าสนใจ ดังนี้
ตัวอย่าง การสร้างลวดลายจากการผสมผสานรูปแบบต่าง ๆ ของการดำเนินการทางคณิตศาสตร์โดยการบวกของเลขโดด 0,1,2
A ไม่หมุน
B การหมุน 90 องศา
C การหมุน 180 องศา
D การหมุน 270 องศา
รูปแบบ** A,A,A,A **
รูปแบบ ** A,B,C,D**
รูปแบบ A,B,B,A
รูปแบบ** D,D,C,C**
รูปแบบ A,A,B,B
รูปแบบ** B,B,B,B**
ตัวอย่าง การสร้างลวดลายจากการผสมผสานรูปแบบต่าง ๆ ของการดำเนินการทางคณิตศาสตร์ โดยการคูณของเลขโดด 0,1,2,3,4,5,6 ( พิจารณารูปแบบ A,B,C และ D ของเลขโดด 0,1,2,3,4,5,6 จากตัวอย่างข้างต้น )
รูปแบบ A,B,C,D
แนวทางการนำผลไปใช้
จากการดำเนินการจัดทำโครงงาน ทางกลุ่มได้มีแนวทางในการนำผลไปใช้ ดังนี้
1. ตารางจัตุรัสที่มีลวดลายสามารถนำมาประยุกต์ได้ในงานหลาย ๆ อย่าง เช่น การออกแบบลวดลาย ผ้าบาติก กระเบื้อง ที่รองจานข้าว Wallpaper เสื้อผ้า ผ้าคอสติส เป็นต้น
2.นำการดำเนินการของโครงงาน ไปประยุกต์ใช้ในการสร้างกิจกรรมที่ส่งเสริมความคิดสร้างสรรค์ และส่งเสริมใช้เวลาว่างให้เกิดประโยชน์ เช่น การประกวดการออกแบบลวดลายทางคณิตศาสตร์ เป็นต้น
การอภิปรายผล** และข้อเสนอแนะ**
อภิปรายผล
1. จากการดำเนินการทางคณิตศาสตร์ตามลักษณะการเดินของนาฬิกา จะพบว่า ทางกลุ่มได้ศึกษาในการดำเนินการ ได้แก่ การบวก การลบ การคูณ เท่านั้น ส่วนการหารนั้นจะพบว่ามีบางจำนวนที่ดำเนินการหารแล้ว ผลที่ได้เป็นเศษส่วนหรือทศนิยม ซึ่งอยู่นอกเหนือจากชุดเลขโดดที่ทางกลุ่มกำหนด
2. ชุดของเลขโดดที่มากขึ้น เมื่อกำหนดสีในแต่ละเลขโดด ทำให้ตารางจัตุรัสที่ได้มีรูปแบบที่สวยงามขึ้น
3. การหมุนหรือพลิกตารางจัตุรัสแต่ละครั้ง ทำลวดลายจะแตกต่างกันไปในจำนวนที่จำกัด
4. การสร้างรูปแบบลวดลาย จากการหมุนหรือพลิกตารางจัตุรัสนั้นมีหลากหลายมากกว่าที่ทางกลุ่มได้ให้ตัวอย่างไว้ และยังสามารถสร้างลวดลายต่าง ๆ จากชุดเลขโดดอื่น ๆ ได้
ข้อเสนอแนะ
1. ควรมีตัวอย่างรูปแบบลวดลายให้มากกว่านี้
2. ควรศึกษาในเรื่องสมบัติของการดำเนินการทางคณิตศาสตร์กับลักษณะการเดินของนาฬิกา ทั้งการดำเนินการบวก การลบ และการคูณ ในแต่ละชุดเลขโดด
3. ควรศึกษาผลที่ได้จากการหมุนของตารางจัตุรัสในจำนวนครั้งที่มากขึ้น เช่น ผลของการหมุนตารางจัตุรัส เลขโดด 0 - 3 จำนวน 2 ครั้ง ได้แก่ การหมุน 90 องศา แล้วหมุนต่ออีก 270 องศา เป็นต้น
บรรณานุกรม
กรมวิชาการ กระทรวงศึกษาธิการ. 101 โครงงานคณิตศาสตร์. กรุงเทพฯ : โรงพิมพ์คุรุสภา
ลาดพร้าว, 2540.
สถาบันพัฒนาคุณภาพวิชาการ (พว.). โครงงานคณิตศาสตร์. กรุงเทพฯ : บริษัท เดอะมาสเตอร์กรุ๊ป
แมเนจเม้นท์ จำกัด, 2543.
ขอบคุณมากเยยคร่า
ขอบคุณมากเลยค่ะ โครงงานช่วยได้เยอะเลยค่ะ ^^
คุณทำโครงงานได้ดีมากค่ะ แต่ฉันอยากได้ละเอียดกว่านี้ค่ะ
ปล. คุณเก่งมากจริงๆเลยนะคะ
.....................+++ดีมากคร่าขอบคุณค่ะ
ขอบคุณค๊าฟฟฟฟฟฟฟฟ
คุนทำได้ดีามากจร๊ะเเต่อยากได้ความรุู้มากกว่านี้คะ
☻♣♠♠♠♠♠♠♠♠♠♠♠♠♠♠♠
ขอได้ปะ
ขอบคุณมากๆ :)'
ขอบคุณมากคร่า
ของคุณค่าาาาาาาาาาาาาาาาาาาาาา
222
ขอได้ป่ะ
ีเ้่เ
ดีดีดีดีดีดีดีดีดีดีดีดีดีดีดีดีดีดีดีดีดีดีดีดีดีดีดีดีดีดีดีดีดีดี
ดีขึ้น ok รุ๊เรื่อง บาย
ดีมากค่ะ ง่ายจุงเบย
ดีมากค่ะแต่อยากได้อีก
น่ารักจุงเบย
ขอบคุณนะคะ เพราะเว็บนี้ถึงทำให้หนูสอบผ่านhttp://www.google.co.th/imgres?q=%E0%B8%84%E0%B8%B2%E0%B9%81%E0%B8%A3%E0%B8%84%E0%B9%80%E0%B8%95%E0%B8%AD%E0%B8%A3%E0%B9%8C%E0%B8%9C%E0%B8%B9%E0%B9%89%E0%B8%9E%E0%B8%B4%E0%B8%97%E0%B8%B1%E0%B8%81%E0%B8%A9%E0%B9%8C&hl=th&tbo=d&biw=770&bih=470&tbm=isch&tbnid=eKxAd2Dk3G6FUM:&imgrefurl=http://th-th.facebook.com/earnz.anuluk&docid=n8b2frzE178DwM&imgurl=http://sphotos-a.xx.fbcdn.net/hphotos-ash4/284151_284414715009351_32440093_n.jpg&w=402&h=349&ei=m5YLUe7aHYr4rQeiqYD4DQ&zoom=1&ved=1t:3588,r:53,s:0,i:249&iact=rc&dur=848&sig=115280929154573875420&page=5&tbnh=183&tbnw=211&start=44&ndsp=13&tx=138&ty=134
ดีมากเลย