เรียนสถิติด้วยภาพ ตอนที่ 12 การแจกแจงไคสแควร์
เวลายุ่งเกี่ยวกับจำนวนนับ เขาสอนกันมาว่าให้ใช้ไคสแควร์มาพิสูจน์ว่าจำนวนนับนั้นเป็นไปตามคาดไหม หรือผิดคาด
ก่อนที่จะไปถึงตรงนั้นในมุมมองของนักปฎิบัติ ก่อนอื่นต้องมารู้จักภาคทฤษฎีก่อนว่าไคสแควร์มีที่มายังไง ก็ต้องมาเรียนแนวคิดทางทฤษฎีกันก่อน ว่างั้นเถอะ
ไคสแควร์ เวลาเขียน จะเขียนว่า χ² ซึ่งตัวไคเป็นอักษรกรีก
นิยามของไคสแควร์คือ ผลรวมของค่า Z ยกกำลังสอง เมื่อ Z คือค่าที่เรียกว่า independent standard normal random variable
ชื่อยาวซะเหงื่อตก
มันก็คือ Z score นั่นแหละ
ลองนึกถึงเวลาประกาศคะแนนนักเรียน แต่ละคนก็จะรู้ว่าตัวเองได้คะแนนเท่าไหร่ เทียบเป็น z-score เท่าไหร่
เช่น คะแนนเท่ากับค่าเฉลี่ย ก็จะมี Z = 0
คะแนนเท่ากับค่าเฉลี่ยบวกสาม sd ก็จะมีค่า z = 3 (พวกตัวฟัน - ครองคะแนนสูง ๆ ประจำห้อง)
คะแนนเท่ากับค่าเฉลี่ยลบสอง sd ก็จะมีค่า z = -2 (พวกเรียนอ่อน เป็นฐานให้เพื่อนเหยียบศพเป็นประจำ)
การแจกแจง Z จะมีค่าเฉลี่ยตรงศูนย์ แล้วมี sd เป็น 1
การแจกแจงไคสแควร์ ก็คือจับ Z มายกกำลังสอง
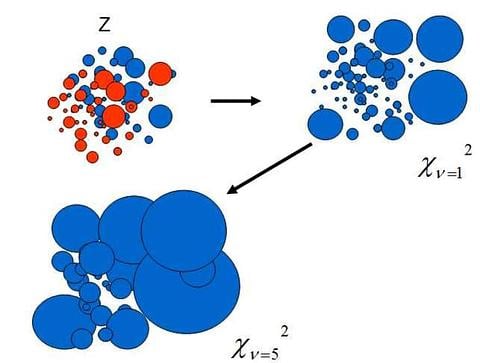
ดูรูปนี้ ที่เขียนว่า Z ถ้าเป็นสีน้ำเงิน คือมีค่้าบวก ถ้ามีสีแดง คือมีค่าลบ
ถ้าขนาด Z เล็ก ๆ ก็จะเป็นวงกลมเล็ก ถ้าขนาด Z ใหญ่ ๆ ก็จะเป็นวงกลมใหญ่
จะเห็นว่า Z ส่วนใหญ่ จะมีขนาดเล็ก ๆ มีปนขนาดใหญ่ ๆ มาบ้างนิดหน่อย (รูปแรกซ้ายบน)
พอจับยกกำลังสอง กลายเป็นไคสแควร์ ค่าที่เคยติดลบ ก็กลายเป็นบวกหมด
ค่าที่ต่ำกว่าหนึ่ง พอยกกำลังสอง ก็จะเล็กจิ๋วลงกว่าเดิมมาก
ค่าที่เกินหนึ่ง พอยกกำลังสอง ก็จะเพิ่มขนาดใหญ่ขึ้นพรวดพราด (รูปแรกขวาบน)
การแจกแจงไคสแควร์ มีสิ่งที่เรียกว่า degree of freedom (D.F.) เข้ามาเกี่ยวข้อง ในที่นี้ ใช้ v แทนค่า D.F.
Degree of freedom ของการแจกแจงไคสแควร์ก็คือ เราสุ่มเอาไคสแควร์กี่ก้อนมารวมกัน
เช่น ถ้า degree of freedom 1 (v=1) ก็จะเป็นตามรูปบนขวา คือเป็นค่า Z กำลังสองแบบอยู่เดี่ยว ๆ
พอเพิ่ม degree of freedom เป็น 5 ก็คือสุ่มก้อนไคสแควร์ตั้งต้นมา 5 ก้อน จับมารวมกัน คราวนี้ ก้อนก็จะใหญ่ขึ้น
โอกาสที่เราหยิบห้าก้อนมาแล้วทุกก้อนเป็นฝุ่นผงทั้งหมด เกิดยาก ทำให้ค่าไคสแควร์ที่มีค่าใกล้ศูนย์แทบจะหาไม่ได้เมื่อเรากำหนด degree of freedom สูง ๆ
โอกาสที่เราหยิบห้าก้อนมาแล้วทุกก้อนเป็นขนาดยักษ์ทั้งหมด ก็เกิดยากเช่นกัน เพราะไม่ใช่ว่ามีก้อนยักษ์อุดมสมบูรณ์นัก ทำให้ค่าไคสแควร์ที่มีค่าเยอะมาก ๆ ก็แทบจะหาไม่ได้เหมือนกัน
แต่ที่เป็นไปได้มากสุดคือ เราหยิบมาทั้งก้อนเล็กและก้อนใหญ่มารวมกัน เกิดเป็นก้อนกลาง ๆ
โอกาสเจอแต่ละขนาดก้อน ก็คือการแจกแจงแบบไคสแควร์นั่นเอง
เมื่อเรามีรูปแบบการแจกแจงไคสแควร์แล้วจะนำตรงนี้ไปใช้ประโยชน์ได้อย่างไร
ง่ายมากครับ
สมมติเราทดลองอะไรมาสักอย่าง คำนวณหาค่าไคสแควร์ที่บรรยายผลการทดลองออกมาได้ค่าหนึ่ง สมมติว่าเป็น k
เราก็มาดูว่า k ผลการทดลองของเรา มีโอกาสเท่าไหร่ที่จะใหญ่กว่าก้อนไคสแควร์แต่ละก้อน
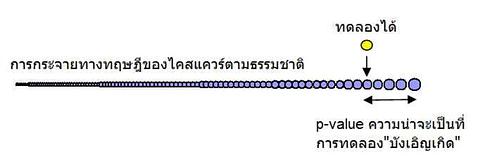
ถ้าไคสแควร์ที่ทดลองได้ ยังอยู่ในช่วงที่เจอตามธรรมชาติ ก็ต้องไม่ใหญ่เกินไป(ดูไปทางด้านขวา) และไม่เล็กเกินไป (ดูไปทางด้านซ้าย)
เช่น จากคลัง 1 ล้านก้อน หากข้อมูลของเรามีไคสแควร์ติด 15 อันดับแรกของก้อนยักษ์ แสดงว่าความน่าจะเป็นหรือ p-value ที่มันเกิดเองตามธรรมชาติได้ จะมีเพียง 15 ในล้าน หรือ p=0.000015
ดังนั้น เราก็ต้องสร้างคลังของการแจกแจงไคขึ้นมา เราต้องรู้ว่าในคลังมีไคสแควร์กี่ก้อน เอาผลการทดลองของเรามาไล่เทียบขนาด เราก็จะรู้ว่า หากของเราติดอันดับ x จาก N ก้อน แสดงว่า p-value คือ x/N

ภาพข้างบน สมมติการทดลองของเรา มี degree of freedom ของการรายงานผลการทดลองเป็น 1 เราก็ไปดูจากคลังก้อนไคสแควร์ที่ degree of freedom = 1 แล้วพบว่า จาก 100 ก้อน มีเพียง 3 ก้อนเท่านั้น ที่ใหญ่กว่า k ของเรา ก็แสดงว่า ค่า p-value = 0.03 (มาจาก 3/100)
ส่วนภาพข้างล่าง การทดลองของเรา มี degree of freedom = 5
เราก็ไปดูจากคลังก้อนไคสแควร์ที่ degree of freedom = 5 หากพบว่า จาก 100
ก้อน มีเพียง 25 ก้อนที่ใหญ่กว่า k ของเรา
ก็แสดงว่า ค่า p-value = 0.25 (มาจาก 25/100)

เวลาเปรียบเทียบค่าไคสแควร์ของการทดลอง กับคลังไคสแควร์ทางทฤษฎี อันที่จริงเราเปรียบเทียบได้สองแบบ
แบบแรกคือ เปรียบเทียบว่าผลของเรา ผิดคาดรุนแรงแค่ไหน (ใช้งานทางสถิติทั่วไปก็ใช้แบบนี้)
แบบที่สองคือ เปรียบเทียบว่าผลของเรา เป็นไปตามคาดมากเกินไปไหม เช่น ดูมันเหมือนทฤษฎีเกินไปจนชวนให้ไม่น่าสบายใจ เช่น มาตรวจสอบว่ามีการปลอมข้อมูลงานวิจัยไหม อะไรทำนองนั้น ที่ทำให้มันดูดีสมบูรณ์แบบอย่างไม่น่าจะเป็นไปได้ (งานวิจัยทั่วไปไม่ค่อยได้ใช้แบบนี้ ถ้าใช้เมื่อไหร่ แสดงว่าเขามีมุมมองบางอย่างเรื่องการตีความผลการทดลองที่ไม่ตรงไปตรงมา ควรอ่านเหตุผลอย่างละเอียดว่านักวิจัยคิดยังไง)
เวลาแปลงเป็นค่า p-value เราไม่ต้องสร้างคลังค่าไคสแคร์เองหรอกครับ โปรแกรมทำให้ได้ครบวงจร คือเราส่งค่าไคสแควร์ของเราไป และบอกแค่ว่าให้เปรียบเทียบกรณีที่ degree of freedom เท่าไหร่ โปรแกรมก็จะคำนวณค่า p-value ออกมาให้ได้เลย ในที่นี้ผมแค่อุปมาให้เห็นภาพเท่านั้นเอง ทำจริงแบบนี้ก็ได้นะ แต่ช้าสุดขีด ไม่ทันกินหรอก
ที่พูดไปแล้ว คือมองในมุมมองทางทฤษฎีว่าการแจกแจงไคสแคร์เป็นอย่างไร แต่ยังไม่ได้มองในมุมมองการปฎิบัติ
ต้องต่อตอนหน้าแล้วละครับ
อาจหลายวันหน่อยนะครับ เพราะผมเล่าด้วยภาพ ไม่ใช่เล่าด้วยคำพูดหรือด้วยสมการ บางทีจะนึกหาภาพที่แทนใจตัวเองได้ ใช้เวลานึกแรมปี ถ้านึกออกเร็วก็มาเล่าต่อเร็ว นึกออกช้า ก็รอกันไป...
สนใจอ่าน เรียนสถิติด้วยภาพ แบบครบทุกตอน เข้าไปที่
http://www.gotoknow.org/posts?tag=เรียนสถิติด้วยภาพ
ความเห็น (0)
ไม่มีความเห็น