Simpson's Paradox, Odds Based (table=โต๊ะ, table=ตาราง)
Simpson's Paradox
บทที่ 10, A collection of power-point presentations
developed from the ActivEpi CD text จาก www.openepi.com
การรวม 2 ตาราง โดยรวมหมวกจากโต๊ะ 2 ตัวไปใว้บนโต๊ะตัวเดียว
OPENEPI, Odds Based Estimates
Odds = Probability that it happen / Probability that it does not
Odds = P / (1 - P)
เช่น Odds ของลูกเต๋าที่จะออกหมายเลขสี่ = 1 : 5 (คือ 1 / 6 หารด้วย 5 / 6)
| Green | Blue | |
| Fit | a | b |
| Not Fit | c | d |
Odds Green = a / c
Odds Blue = b / d
Odds Ratio = Odds Green / Odds Blue
Odds Ratio = ad / bc
Stratum_1 a, b, c, d คือ 5, 8, 1, 2
Stratum_2 a, b, c, d คือ 2, 1, 8, 5
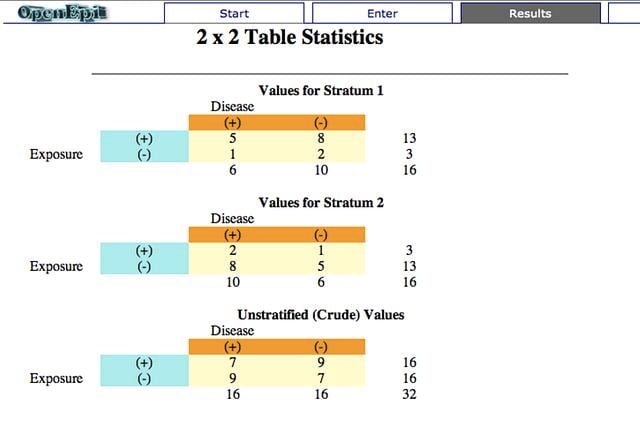
Table 1
Odds Green = 5 : 1 = 5 / 1
Odds Blue = 8 : 2 = 4 / 1
Odds Ratio = 1.25 (95%CI 0.08 to 17.65)
Table 2
Odds Green = 2 : 8 = 0.25 / 1
Odds Blue = 1 : 5 = 0.2 / 1
Odds Ratio = 1.25 (95%CI 0.08 to 17.65)
Unstratified (Crude) รวม 2 โต๊ะเข้าด้วยกัน
Odds Green = 7 : 9 = 0.77 / 1
Odds Blue = 9 : 7 = 1.28 / 1
Odds Ratio = 0.61 (95%CI 0.14 to 2.44)
เมื่อถามว่า "หมวกที่ลูกค้าใส่ได้พอดีมากกว่า สีอะไร"
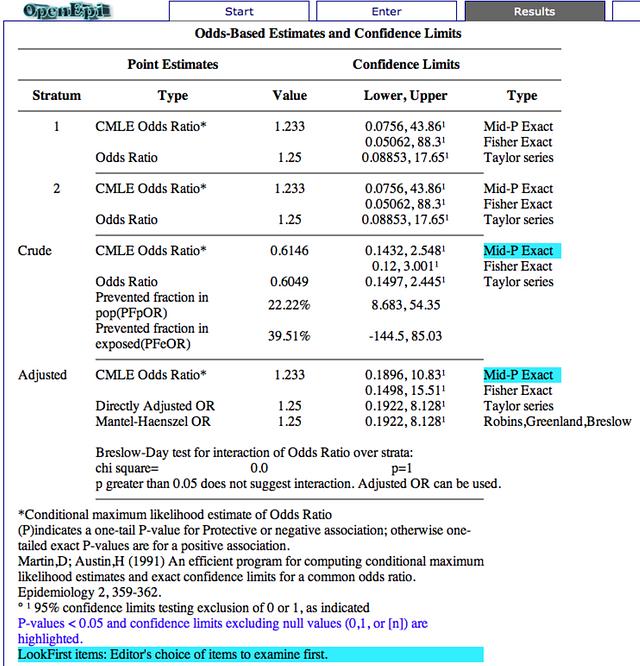
(1) table1 OR = 1.25 (95%CI 0.08 to 17.65) เขียว
(2) table2 OR = 1.25 (95%CI 0.08 to 17.65) เขียว
(3) Crude OR = 0.61 (95%CI 0.14 to 2.44) น้ำเงิน ?
เมื่อรวม (1)+(2) เป็น (3) Crude OR กลับทิศทางกับ OR ของ (1) และ (2)
(4) M-H Adjusted OR = 1.25 (95%CI 0.19 to 8.12) เขียว
Openepi แนะนำ Adjusted OR วิธี Mid-P Exact
การรวม Table แบบ Crude ผลกลับทิศทางกับ table1 และ table2
ใช้ Adjusted OR ปรับแก้ ผลจึงไปทิศทางเดียวกัน
p > 0.05 ไม่น่าจะมี Interaction ใช้ Adjusted OR ได้
แต่ว่าทั้ง 4 แบบ 95%CI มี 1 รวมอยู่ด้วย OR มีโอกาส=1
Crude OR ให้ผลกลับทิศทาง กับการแยกคิด OR ทีละกลุ่มเดียว
ใช้ Adjusted Odds Ratio จะถูกต้องมากกว่า
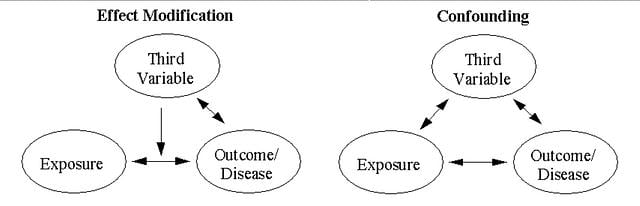
แต่ต้องดูที่ Effect Modification และ Confounding ด้วย
การรวมกันแบบ Crude บางครั้งจะไม่ถูกต้อง
เพราะมี Effect Modification หรือ Confounding หรือมีทั้งสองอย่าง
Openepi :ในส่วน
Kevin's Webpage
http://www.sph.emory.edu/~cdckms/
http://www.sph.emory.edu/~cdckms/CONF2f.zip
Extract ได้ เป็น CONF2f.doc 22-Jun-2005
Page 14/33 อธิบาย confounding และ effect modification
สำหรับโปรแกรม STATA
จะเรียง a, b, c, d โดยที่ Exposed และ Unexposed อยู่ด้านบน, Cases และ Controls จะอยู่ด้านซ้ายของ 2x2 table (Kleinbaum; Breslow/Day Layout)
y คือ row (0=Control, 1=Cases)
x คือ column (0=Unexposed, 1=Exposed)
pop คือ จำนวน นำมา frequency weight [fw=pop]
gr คือ group แยกแต่ละ strata (0, 1)

คำสั่ง STATA ให้คำนวณ Odds Rato แยกทีละ group, รวมกันแบบ Crude ซึ่งจะแสดง a, b, c, d ใน 2x2 table, Exposed และ Unexposed อยู่ด้านบน Cases และ Controls อยู่ด้านซ้าย และวิธี M-H ซึ่งจะแสดง OR ของ gr_1, gr_2, Crude และ M-H (วิธี M-H จะไม่ได้แสดง 2x2 table)
.cc y x [fw=pop] if gr==0
.cc y x [fw=pop] if gr==1
.cc y x [fw=pop]
.cc y x [fw=pop] , by(gr)
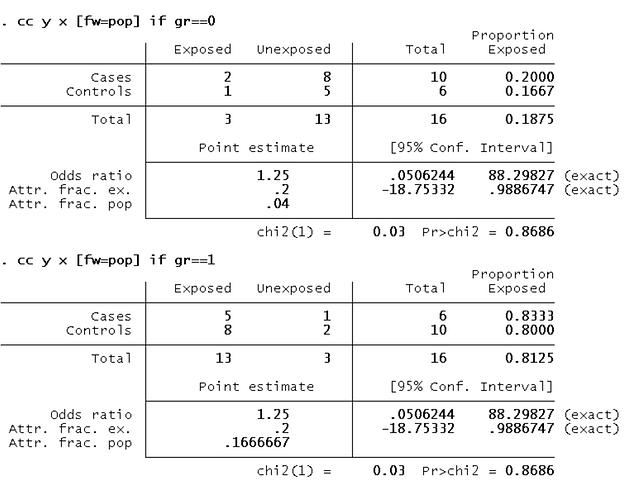
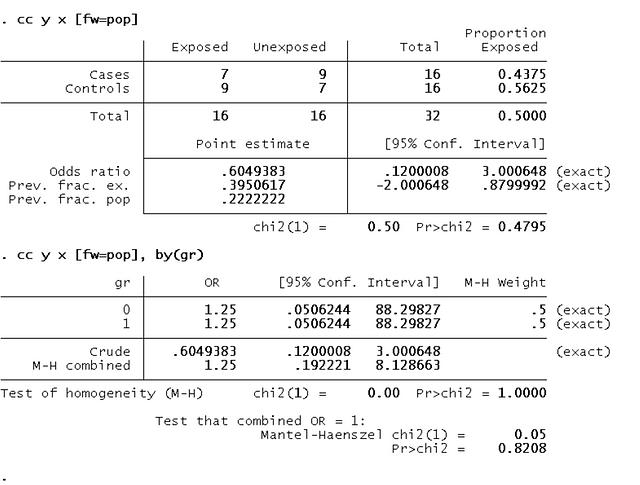
1) gr_0 OR=1.25 95%CI 0.05 to 88.29
2) gr_1 OR=1.25 95%CI 0.05 to 88.29
3) Crude OR=0.60 95%CI 0.12 to 3.00
4) M-H Adjusted OR=1.25 95%CI 0.19 to 8.12
แต่ 95%CI ของ OR ของ gr_0, gr_1, Crude และ M-H มี 1 รวมอยู่ด้วย
คือ OR มีโอกาสเท่ากับ 1 ได้
=======================================
Simpson's Paradox คำนวณแบบ Risk Based
http://www.gotoknow.org/blogs/posts/461915
Simpson's Paradox
การรักษานื่วในไต ตัวอย่างจาก Clinical Trial
http://www.ncbi.nlm.nih.gov/pmc/articles/PMC1339981/pdf/bmjcred00227-0031.pdf
1) นิ่วก้อนเล็ก วิธี A ดีกว่า
2) นิ่วก้อนใหญ่ วิธี A ดีกว่า
3) Crude นับรวมกันทั้งนิ่วก้อนเล็กและนิ่วก้อนใหญ่ วิธี B ดีกว่า ?
4) Adjusted Odds Ratio โดยโปรแกรม Openepi และ STATA
http://www.gotoknow.org/blogs/posts/439144
ความเห็น (6)
แต่ละชั้นคือ "Strata" Strata_1 คือ โต๊ะที่ 1 Strata_2 คือ โต๊ะที่ 2
การรวมเข้าด้วยกัน "อย่างหยาบ" คือ Crude
สามารถปรับแก้ไข เช่น ใช้วิธี M-H Adjusted
ถ้าได้ข้อมูลแบบรวมกลุ่มมาก่อน สามารถนำมาแยกวิเคราะห์ เรียก "Stratified Analysis"
ถ้า Sample size คำนวณมาสำหรับคำถามหลัก เมื่อแยก Strata
จำนวนนับของแต่ละ Strata อาจน้อยลง ทำให้ 95% CI มี 1 รวมอยู่ด้วย
คือจากการคำนวณได้ค่า Odds Ratio 1.25
มั่นใจที่ 95% ว่า Odds Ratio มีค่าระหว่าง 0.19 to 8.12
95% CI มี 1 รวมอยู่ด้วย
คือ Odds Ratio ของ Strata_1 หารด้วย Odds Ratio ของ Strata_2 อาจจะมีค่าเป็น 1 ได้
อาจารย์นภดลคะ
รบกวนสอบถามค่ะว่า simpson's paradox นี่เป็นตัวป่วนเหมือนกับ confounder เลยใช่ไม๊คะ ไม่ทราบว่าสองตัวนี้มีความแตกต่างกันอย่างไรคะ เพราะเวลาวิเคราะห์หา OR , เมื่อได้ crude OR แล้วแยกตารางก็ได้ผลขัดแย้งกัน เมื่อพิจารณาอีกตัวแปร เช่น ต้องการหา survival rate ของ smoker, nonsmoker
พอเพิ่ม อายุ เข้าไป กลับให้ผลขัดแย้งกันไปเลย ดังนั้นอายุเป็น simpsson's paradox และก็ยังเป็น confounder
ขอบพระคุณค่ะ
เมื่อวิเคราะห์แยก strata มักจะเป็นเหมือนที่ถามมาครับ
http://www.openepi.com/v37/TwobyTwo/TwobyTwo.htm
2x2 table ใน OpenEpi สามารถเพิ่ม strata ไดอีก
เช่น เพิ่ม table 2 และ เพิ่ม table 3 เมื่อ กด calculate
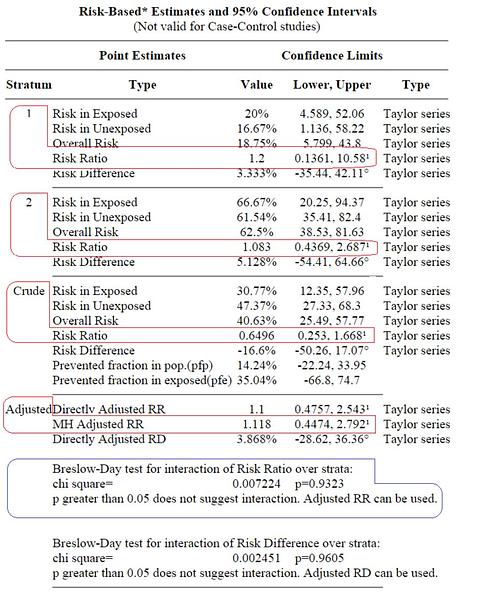
จะมีส่วนนี้ เพิ่มมา "Breslow-Day test for interaction"
ว่า เป็น interaction หรือว่าไม่น่าจะเป็น interaction
และควรจะใช้ adjusted Risk Ratio ได้หรือไม่ (หรือจะใช้ Risk Difference ได้หรือไม่)
| Breslow-Day test for interaction of Risk Ratio over strata: | |||||||
| chi square= | p greater than 0.05 does not suggest interaction. Adjusted RR can be used. | ||||||
| p greater than 0.05 does not suggest interaction. Adjusted RR can be used. |
| Breslow-Day test for interaction of Risk Difference over strata: | |||||||
| chi square= | p greater than 0.05 does not suggest interaction. Adjusted RD can be used. | ||||||
แต่เมื่อแบ่งกลุ่มย่อย ลงไปอีก จะทำให้แต่ละกลุ่ม มีจำนวนน้อยลง
จนทำให้ 95% CI ของ RR มี 1 รวมอยู่ด้วย หรือ 95% CI ของ RD มี 0 รวมอยู่ด้วย
ดังนั้น อาจจะคำนวณทั้งหมด และรายงานผล (ตอบคำถามหลัก)
และแยกกลุ่มเท่าที่คาดหมายว่า อาจจะทำให้เปลี่ยนแปลงผลไปจากเดิม
(อาจตอบคำถามรองได้บางคำถาม)
ไมจำเป็นต้องตัด interaction ออก เพียงแต่ให้รู้ว่ามี interaction อยู่
แต่ควรออกแบบวิธีเก็บข้อมูล เพิ่อให้ไม่มี confounder
http://www.gotoknow.org/posts/462228
ตัวแปรที่ 3 เป็น Categorical ที่ใช้แยกกลุ่ม
เช่น กลุ่มอายุ ทำให้ผลเปลี่ยนไป
โดยที่ Adjusted Relative Risk ต่างจาก Crude Realtive Risk
ตัวแปรที่ 3 กลุ่มอายุ ก็คือ Confounder
Confounder ที่พบบ่อย เช่น เพศ กลุ่มอายุ อาชีพ เชื้อชาติ
และ Confounder ต้องมี Association กับ Predictor และ Outcome
ถ้าพบว่ามี Interaction (หรือตัวแปรทีเป็น Effect Modification)
ต้องระวังว่า Confounder อาจไม่ใช่สิ่งที่เกิดขึ้นจริง
ในการศึกษา Predictor และ Outcomes จึงควรตรวจสอบว่า
มี Interaction หรือไม่ ? มี Confounder หรือไม่ ?
และพิจารณาว่าควรต้อง Adjusted หรือไม่
(Adjusted แล้วเกิดผลดี หรือเพิ่มความคลาดเคลื่อน)
ในแต่ละ data set
อาจจะมีทั้ง Interaction และ Confounding (data set 1)
หรือมีแต่เพียง Interaction (data set 2, 3)
หรือมีแต่เพียง Confounding (data set 4)
หรือว่าไม่มี Interaction และ Confounding (data set 5)
ถ้ามี Interaction มาก Confounding อาจจะไม่ใช่สิ่งที่เป็นจริง (data set 2,3)
Stratified table
RR ของ Stratum 1, Stratum 2 ต่างกันก็คือมี Interaction (data set 1, 2, 3)
RR ของ Stratum 1, Stratum 2 ไม่ต่างกันก็คือไม่มี Interaction (data set 4, 5)
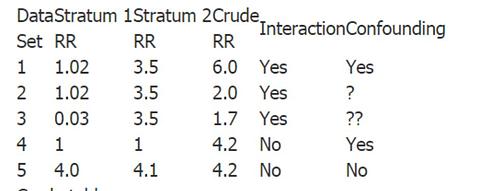
| Data Set |
Stratum 1 RR |
Stratum 2 RR |
Crude RR |
Interaction | Confounding |
| 1 | 1.02 | 3.5 | 6.0 | Yes | Yes |
| 2 | 1.02 | 3.5 | 2.0 | Yes | ? |
| 3 | 0.03 | 3.5 | 1.7 | Yes | ?? |
| 4 | 1 | 1 | 4.2 | No | Yes |
| 5 | 4.0 | 4.1 | 4.2 | No | No |
Crude table
Crude RR ถ้่าต่างกับ Stratum1, Stratum2 คือมี Confounding (data set 1, 4)
Crude RR ถ้่าไม่ต่างกับ Stratum1, Stratum2 คือไม่มี Confounding (data set 5)
http://www.gotoknow.org/blog/epistat/461915
Risk Ratio (RR)
Breslow-Day test for interaction of Risk Ratio over strata
Two main complications of analysis of single exposure effect
(1) Effect modifier (2) Confounding factor
www.msu.edu/~fuw/teaching/Fu_Ch13_2_DesignAnal.ppt
Confounder ที่เห็นชัดคือ dataset 4
RR1 =1, RR2 =1 ตัวแปรต้นเปลี่ยน ไม่ทำให้ ตัวแปรตาม เปลี่ยนแปลงเลย
รวมกันแบบ Crude RR เป็น 4.2 Confounder รู้ว่าเป็น Confounder ในขั้นตอนวิเคราะห์
(ถ้าจะทำวิจัยใหม่ ตัดออกแต่แรกจะดีกว่า)
dataset 1 มี ทั้ง Confounder และ Interaction
ถ้าทำ ฺBreslow-Day test ถ้า p-Value < 0.05 คือน่าจะมี Interaction
คำสั่ง สำหรับ Odds Ratio คือ .cc var1 var2, by(gr) bd
แต่ถ้าใช้กับ Risk Ratio สั่ง .cs var1 var2, by(gr) bd จะขึ้นว่า option not allowed
https://dl.dropboxusercontent.com/u/1999671/EPI_56...