ครั้งที่ 13 "สถิติที่ใช้กันมากในงานวิจัย". ## (1) ## สถิติบรรยาย
1. ร้อยละ (Percentage)
มักนิยมเรียกว่า เปอร์เซ็นต์ ใช้สัญลักษณ์ คือ … %...
ตัวอย่าง จากการสำรวจนิสิตระดับปริญญาตรี ที่เรียนหลักสูตรการผลิตครู 5 ปี ประจำปีการศึกษา 2553 ของมหาวิทยาลัยนเรศวร
จำนวน 250 คน เป็นนิสิตชาย จำนวน 110 คน และนิสิตหญิง จำนวน 140 คน
จงคิดจำนวนของนิสิตชายและนิสิตหญิงเป็นเปอร์เซ็นต์
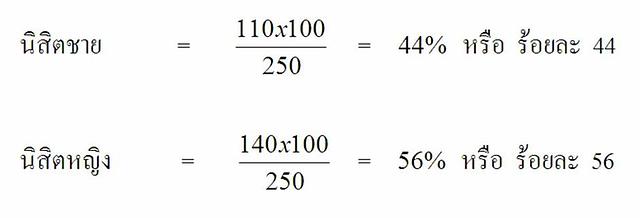
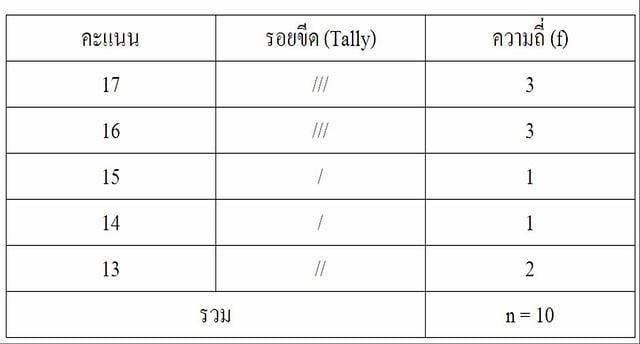
2. การแจกแจงความถี่ (Frequency Distribution) มี 2 ลักษณะ คือ
2.1 การแจกแจงความถี่แบบไม่จัดกลุ่ม
เช่น คะแนนสอบวิชาชีววิทยาของนักเรียน 10 คน เป็นดังนี้ 17 16 17 17 16 13 16 15 14 13
2.2 การแจกแจงความถี่แบบจัดกลุ่ม
3. การวัดแนวโน้มเข้าสู่ส่วนกลาง (Measure of Central Tendency)
: เป็นการหาค่ากลางเพื่อเป็นตัวแทนของข้อมูล นิยมใช้ 3 วิธี ได้แก่
3.1 ค่าเฉลี่ย (Mean) หรือค่ามัชฌิมเลขคณิต (Arithmetic mean)
: เป็นการนำข้อมูลทั้งหมดมารวมกัน แล้วหารด้วยจำนวนข้อมูล
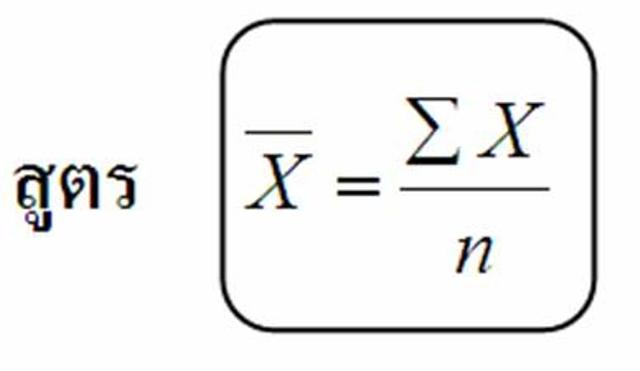ΣX = ผลรวมของคะแนนทั้งหมด n = จำนวนคะแนน หรือข้อมูลทั้งหมด
ตัวอย่าง คะแนนสอบวิทยาศาสตร์ของนักเรียนจำนวน 10 คน เป็นดังนี้ 15 14 13 9 13 12 11 17 10 18
สามารถคำนวณหาค่าเฉลี่ยของคะแนนได้ ดังนี้
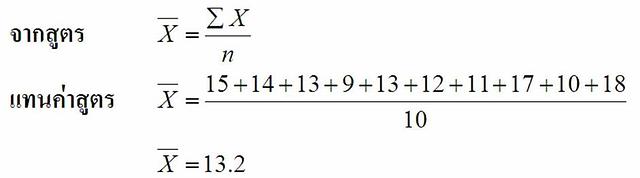
3.2 มัธยฐาน (Median) สัญลักษณ์ Mdn หรือ Md
: เป็นคะแนนที่อยู่ตรงกึ่งกลางของข้อมูลทั้งหมด เมื่อนำข้อมูลทั้งหมดมาเรียงลำดับจากมากไปน้อย หรือ น้อยไปมาก
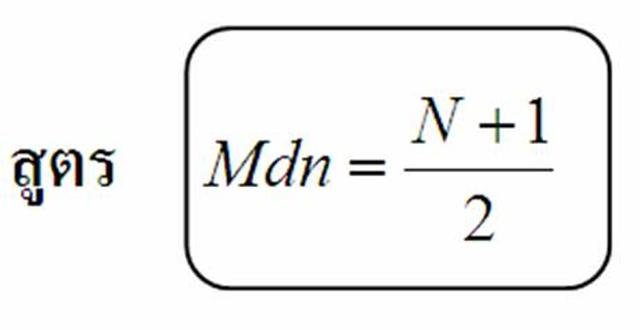n = จำนวนข้อมูลทั้งหมด
ตัวอย่าง คะแนนสอบภาษาไทยของนักเรียนจำนวน 7 คน เป็นดังนี้ 2 3 4 5 6 7 8 และ
คะแนนสอบภาษาต่างประเทศของนักเรียนจำนวน 8 คน เป็นดังนี้ 3 4 5 6 7 8 9 10
คะแนนสอบวิชา ภาษาไทย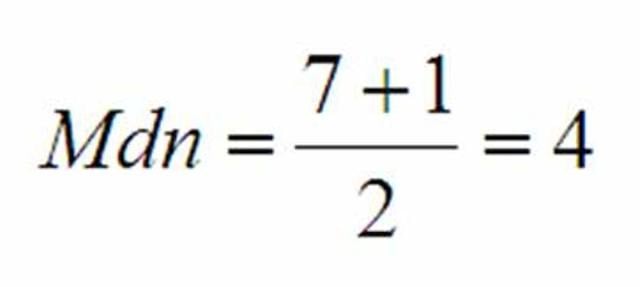 
ดังนั้นมัธยฐาน คือ ลำดับที่ 4 ได้แก่ "5"
คะแนนสอบวิชา ภาษาต่างประเทศ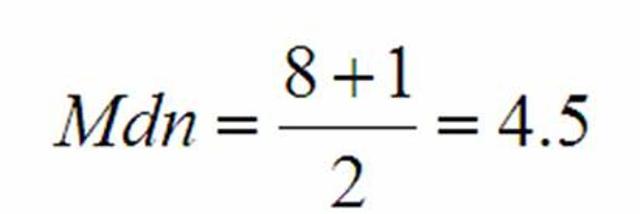 
ดังนั้นมัธยฐาน คือ ลำดับที่ 4 และ 5 ได้แก่ "6" กับ "7"
ดังนี้ 
3.3 ฐานนิยม (Mode)
: เป็นค่าที่มีความถี่สูงที่สุด
: สัญลักษณ์ คือ Mo
ตัวอย่าง คะแนนสอบวิชาสังคมศึกษาของนักเรียนจำนวน 10 คน เป็นดังนี้ 9 10 11 11 11 13 13 14 15
จะมีฐานนิยมเป็นเท่าใด
ฐานนิยม จะเป็น 11 เนื่องจากมีค่าความถี่สูงสุด คือ ความถี่เท่ากับ 3
4. การวัดการกระจาย (Measure of variability)
: เป็นการหาค่าการกระจายของข้อมูล หากข้อมูลมีความแตกต่างกันมากค่าการกระจายจะสูง หากคะแนนมีความใกล้เคียงกัน
ค่าการกระจายจะต่ำ
4.1 พิสัย (Range) สัญลักษณ์ คือ R
: เป็นค่าความแตกต่างของข้อมูลสูงสุดและข้อมูลต่ำสุด
ตัวอย่างที่ 1. ข้อมูลชุดหนึ่งมีค่า 15 14 13 9 12 11 17 10 10 18 ข้อมูลชุดนี้มีพิสัยเท่าใด
จากข้อมูล ค่าสูงสุด คือ 18 , ค่าต่ำสุด คือ 9
พิสัย (R) = 18 - 9 = 9
ตัวอย่างที่ 2. ข้อมูลชุดหนึ่งมีค่า 10 10 10 10 10 10 10 10 ข้อมูลชุดนี้มีพิสัยเท่าใด
จากข้อมูล ค่าสูงสุด คือ 10 , ค่าต่ำสุด คือ 10
พิสัย (R) = 10 - 10 = 0
4.2 ค่าเบี่ยงเบนมาตรฐาน (Standard Deviation) สัญลักษณ์ คือ S.D.
: เป็นค่ารากที่สองของความแปรปรวน
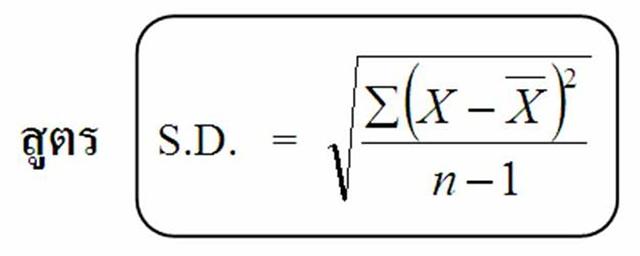
ตัวอย่างที่ 1. จงหาส่วนเบี่ยงเบนมาตรฐานของข้อมูลต่อไปนี้ 8 6 7 4 10
วิธีการ
ขั้นที่ 1 หาค่าเฉลี่ย 
= 7
ขั้นที่ 2 สร้างตาราง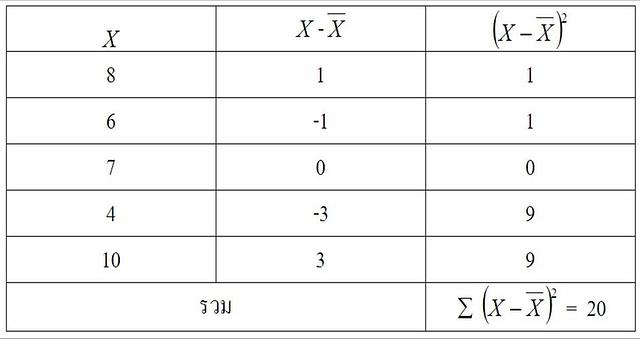 
ขั้นที่ 3 แทนค่าในสูตร
ส่วนเบี่ยงเบนมาตรฐาน
5. ค่าสหสัมพันธ์ (Correlation Coefficient)
: เป็นค่าที่บอกความสัมพันธ์ระหว่างตัวแปร 2 ตัว
: ค่าสัมประสิทธิ์สหสัมพันธ์ มีค่าระหว่าง -1 ถึง +1
5.1 สัมประสิทธิ์สหสัมพันธ์แบบเพียร์สัน (Pearson Product Moment Correlation Coefficient)
: ใช้เมื่อข้อมูล 2 ชุด อยู่ในระดับช่วง (Interval Scale) ขึ้นไป
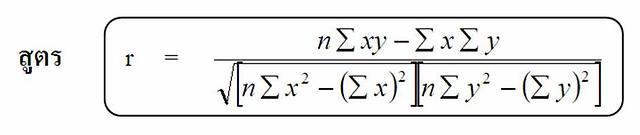
ตัวอย่าง นักศึกษาจำนวน 10 คน สอบวิชาวิจัยและวิชาวัดผล ได้คะแนน
ดังตาราง จงคำนวณหาค่าสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สัน
แสดงว่า คะแนนวิชาวิจัยและวิชาวัดผลมีความสัมพันธ์กันสูง ทางบวก
5.2 สัมประสิทธิ์สหสัมพันธ์แบบอันดับที่ของสเปียร์แมน (Spearman’s Rank Correlation Coefficient)
: ใช้เมื่อข้อมูล 2 ชุด อยู่ในระดับจัดอันดับ (Ordinal Scale)
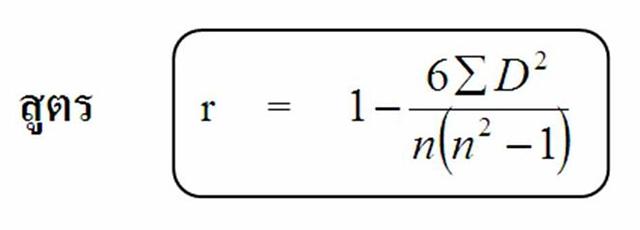D = ผลต่างอันดับที่ของข้อมูลแต่ละคู่
n = จำนวนข้อมูลที่ได้รับการจัดอันดับ
ตัวอย่าง ผู้เชี่ยวชาญ 2 ท่าน จัดอันดับการประกวดโรงเรียนคุณธรรม จากโรงเรียนที่เข้าประกวดทั้งหมด 5 โรงเรียน
ได้ผลดังตาราง ต่อไปนี้
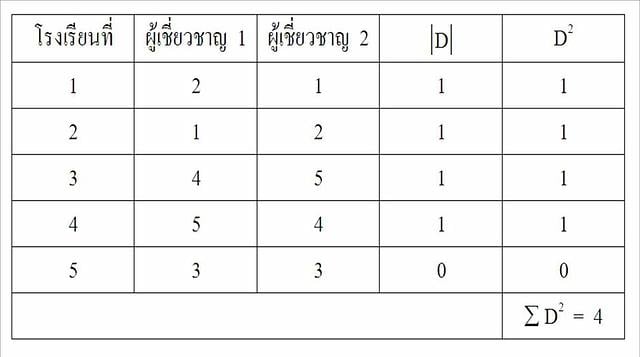
จากสูตร 
แทนค่าสูตร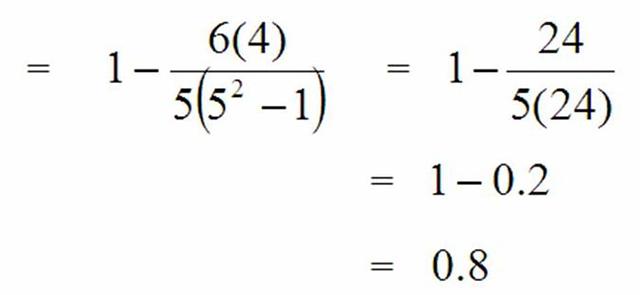 
แสดงว่า การจัดอันดับของผู้เชี่ยวชาญ 2 ท่าน มีความสัมพันธ์ (สอดคล้อง) กันค่อนข้างสูง (ทางบวก)
5.3 สัมประสิทธิ์สหสัมพันธ์แบบอันดับที่ของเคนดอลล์ (Kendall’s Rank Correlation Coefficient)
: วิธีคล้ายของสเปียร์แมน จะใช้เมื่อผู้ให้ข้อมูล (ผู้เชี่ยวชาญ) 3 ท่าน ขึ้นไป
สูตร 
D = ผลต่างระหว่างผลรวมอันดับที่แต่ละคนกับค่าเฉลี่ยของผลรวมอันดับที่
k = จำนวนผู้จัดอันดับ
n = จำนวนข้อมูลที่ได้รับการจัดอันดับ
ตัวอย่าง ผู้เชี่ยวชาญ 3 ท่าน จัดอันดับการประกวดโรงเรียนคุณธรรม จากโรงเรียนที่เข้าประกวดทั้งหมด 5 โรงเรียน
ได้ผลดังตาราง ต่อไปนี้
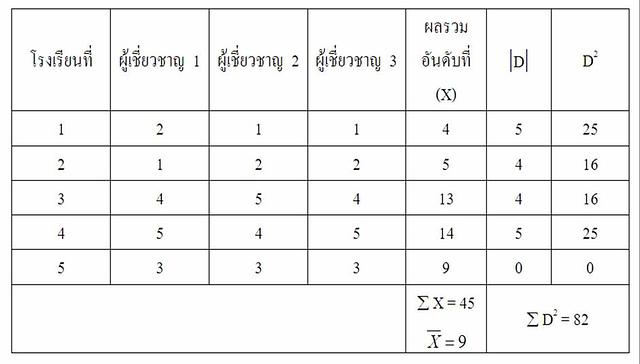
วิธีการ
(1) ผลรวมอันดับที่ (X)
หาจาก การนำคะแนนของผู้เชี่ยวชาญแต่ละคนมาบวกกัน
ตัวอย่าง โรงเรียนที่ 1 คิดจาก 2 + 1 + 1 = 4
โรงเรียนที่ 5 คิดจาก 3 + 3 + 3 = 9
(2) |D|
หาจาก การนำคะแนน ผลรวมอันดับที่ (X) มาลบด้วย
ตัวอย่าง โรงเรียนที่ 1 คิดจาก 4 – 9 = |-5| = 5
โรงเรียนที่ 5 คิดจาก 9 – 9 = |0| = 0
3) D^2
หาจาก การนำคะแนน |D| มายกกำลังสอง
ตัวอย่าง โรงเรียนที่ 1 คิดจาก 5^2 = 25
โรงเรียนที่ 3 คิดจาก 4^2 = 16
(4) หาผลรวมของ D^2 = 25 + 16 + 16 + 25 + 0 = 82
จากสูตร
แสดงว่า การจัดอันดับของผู้เชี่ยวชาญ 3 ท่าน มีความสัมพันธ์ (สอดคล้อง) กันค่อนข้างสูง (ทางบวก)
ความเห็น (6)
ดีแล้วครับ มันเป็นความรู้ที่ดีและสามารถนำเอาไปเผยแพร่
ขอบคุณครับได้เข้าใจมากขึ้นครับ
ด้วยความยินดีค่ะ
เขียนดีมากๆเลยครับ ขอบคุณมากครับ
ขอบคุณทุกท่านที่มาอ่านค่ะ หวังว่าจะเป็นประโยชน์ได้ไม่มากก็น้อยนะคะ